Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 58
Um barco a vela está deslocando-se para leste a 8,0 mph. O vento parece soprar do Sudoeste, a 12,0 mph, para o velejador.
a. Quais são a rapidez e a orientação verdadeiras do vento?
b. Quais são as verdadeiras rapidez e orientação do vento se ele parece soprar do Nordeste a 12,0 mph?
Passo 1
Seguindo uma roda dos ventos simplificada com as direções norte (N), sul (S), leste (L) e oeste (O) podemos esquematizar os vetores
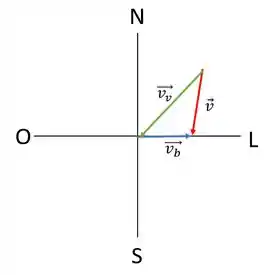
Em que é a velocidade do vento, é a velocidade do barco e é o vetor resultante
E sabemos que o barco
A velocidade do vento é
Passo 2
a. Primeiro temos que descobrir o ângulo em que o vento está se dirigindo
Mas com a velocidade do barco indo em relação a x, temos
Somando os vetores da velocidade
Descobrimos o ângulo que é
E descobrindo o módulo da velocidade
Passo 3
b. Nesse caso, os valores não mudam, mas muda a direção, então mudamos consequentemente seno e cosseno, chegando nos vetores
E o ângulo vai ser
O módulo da velocidade é de
Resposta
- e sudoeste
- 8,5 mph e do Nordeste