Enunciado
Física - Halliday - Vol 3- Ed: 4º - Capítulo 34.Questionário - Ex. 3
Como determinai- a polaridade de um imã não-marcado?
Passo 1
Falaaaa moçadinha, show de bola?
Como diz o Homem de ferro “Eu tenho um plano. Ataque!”
Bora atacar esse problemaaaaaaa junto comigoo.
Muitos ímãs disponíveis para compra não têm seus pólos norte e sul rotulados, o que pode ser um problema, principalmente ao ensinar às crianças as posições dos pólos magnéticos norte e sul.
Passo 2
Existem vários métodos que você pode usar para identificar a polaridade de ímãs não marcados:
Com um pedaço de barbante
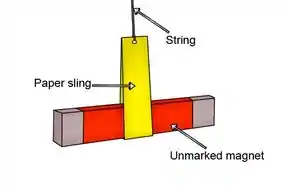
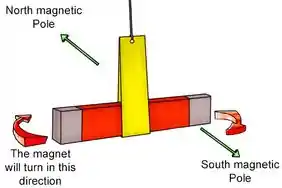
O método tradicional de descobrir a polaridade de um ímã não marcado envolve prender o ímã a um pedaço de barbante com a ajuda de um estilingue de papel.
Você também precisará de uma bússola para esta tarefa.
Se você segurar a ponta do barbante e permitir que o ímã se mova livremente, ele se alinhará com os pólos magnéticos norte e sul, que podem ser identificados por uma bússola.
Passo 3
Usando outro imã
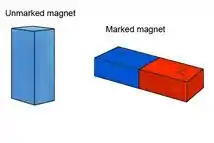
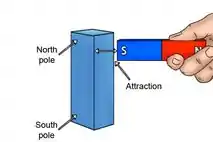
Outra forma de testar a polaridade de um ímã não marcado é usar um ímã já marcado para destacar os pólos norte e sul.
O imã marcado se atrai para o pólo oposto do imã não marcado. Por exemplo, o polo sul do imã marcado se unirá ao polo norte do imã não marcado
Passo 4
Com uma bússola
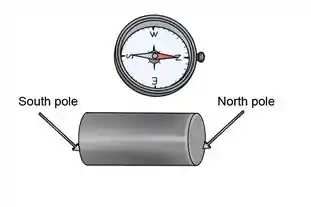
O uso de uma bússola também pode ajudar na identificação dos polos norte e sul de um ímã.
Quando você coloca uma bússola ao lado de um ímã, o pólo norte do ímã seguirá a linha do pólo norte da bússola.
“Às vezes é preciso aprender a correr antes de começar a andar”
Resposta
Resposta nos passos.