Qual deve ser o índice de refração de uma esfera transparente para que os raios paraxiais provenientes de um objeto no infinito sejam focalizados no vértice da superfície oposta ao ponto de incidência?
Passo 1
Vamos começar com um desenho da situação. A ideia é que os raios paralelos sejam todos focalizados em um ponto, desse jeito aqui:
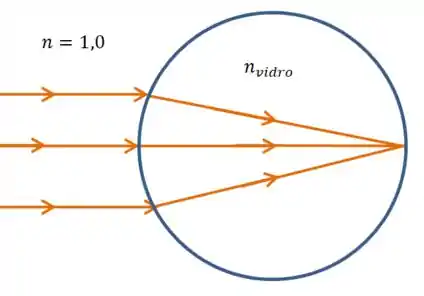
Aqui não tem segredo, vamos usar essa equação aqui:
Passo 2
O próprio enunciado já disse que a gente tem que supor que os raios estão vindo do infinito, então:
Com isso, a primeira fração da nossa fórmula vai tender a zero:
E como a ideia é formar a imagem do outro lado da esfera, a posição da imagem vai ser igual ao diâmetro dela, então:
Essa é a distância do ponto onde a luz incide até o ponto onde os raios se encontram. Então:
Os índices de refração já estão lá no desenho:
Vamos isolar o índice de refração :
Pronto! Esse tem que ser o índice de refração do vidro se você quiser ter aquela situação que representamos no desenho.
Resposta
O índice de refração do vidro deve ser .