Os raios de curvatura de uma lente delgada convergente em forma de menisco são dados por e . Seu índice de refração é . (a) Determine a posição e o tamanho da imagem de um objeto em forma de seta com altura de , perpendicular ao eixo da lente, situado a uma distância de à esquerda da lente. (b) Uma segunda lente delgada convergente, com a mesma distância focal, é colocada a uma distância de à direita da primeira lente. Determine a posição e o tamanho da imagem final. A imagem final é direita ou invertida em relação ao objeto original? (c) Repita o item (b) considerando a segunda lente a uma distância de à direita da primeira lente e mantendo inalterados os demais valores.

(a) Beleza, começando pela primeira lente. Nesse caso, o objeto é colocado a da lente:

Ok, essa é a posição da imagem, agora falta a altura:

(b) Essa imagem aí de cima vai servir como objeto para a segunda lente.

A segunda lente fica à direita da primeira. E a imagem da primeira fica à direita dela.

Ou seja, a distância da primeira imagem até a segunda lente é:

Essa é a única diferença em relação ao passo de cima! Fora isso a gente pode seguir os mesmos passos.

Primeiro vamos pegar a posição da imagem final:

E então a altura:

Lembrando que essa ampliação vai agir sobre a imagem de de altura.

Então a imagem final tem de altura e é direita em relação ao objeto original.

(c) Agora é só repetir o que foi feito no item (b), só que agora a segunda lente está à direita da primeira.

Um desenho pode ajudar bastante aqui. No caso anterior a situação era a seguinte:

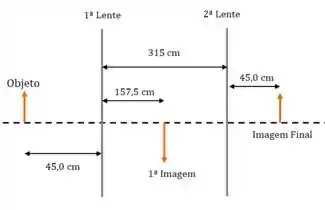
E agora a gente vai trazer a 2ª lente mais para a esquerda:

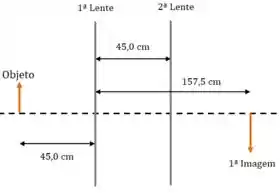
Então agora a posição do objeto é:

E a posição da imagem vai ser:

Isso quer dizer que a imagem final ficaria à esquerda da segunda lente (lado oposto ao do objeto).

E a altura é:

E a imagem continua sendo direita em relação ao objeto original.