Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 18.Problemas Adicionais - Ex. 96
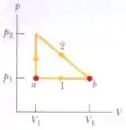
O diagrama da figura mostra duas trajetórias ao longo das quais uma amostra de gás pode passar do estado para o estado , onde . A trajetória requer que uma energia igual a seja transferida ao gás na forma de calor. A trajetória requer que uma energia igual a seja transferida ao gás na forma de calor. Qual é a razão ?
Passo 1
Vamos começar relembrando a primeira lei da termodinâmica:
No caso da trajetória , o calor transferido ao gás deve ser , então:
E é a variação de energia interna entre os pontos e , e é o trabalho realizado na trajetória .
Passo 2
No caso da trajetória , o calor transferido ao gás deve ser , então:
Onde é o trabalho realizado na trajetória . Então ficamos com um sistema de duas equações:
Tirando proveito do fato de que a variação de energia interna é a mesma nos dois caos, vamos subtrair a segunda equação da primeira:
Passo 3
Perceba que o termo do lado direito da equação (o trabalho “resultante” realizado no ciclo) é igual à área definida pelo triângulo do gráfico no enunciado, então:
Mas o enunciado diz que , então:
Agora vamos substituir isso na equação de cima:
Vamos dividir os dois lados por :
Resposta
A razão entre as pressões é .