Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 9.Problemas - Ex. 19

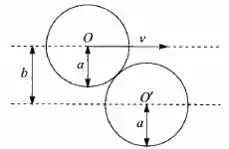
Um disco circular de raio a, que se desloca sobre um colchão de ar com velocidade v e atrito desprezível, colide com um disco idêntico em repouso. O parâmetro de choque é b. a) Considere a colisão no referencial do CM. Levando em conta que a força de contato entre os discos no instante da colisão está dirigida segundo a linha que une os dois centros O e O’, determine o ângulo de que se desviam os momentos dos dois discos nesse referencial. B) Determine as direções e magnitudes das velocidades dos dois discos após a colisão, no referencial do laboratório.

Passo 1

  1. Vamos começar com um esboço do problema

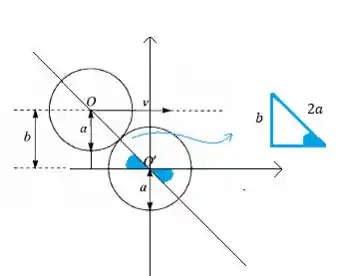
    2. Aqui a partícula 1 é a de baixo e a 2 é a de cima, ok?

    O nosso ângulo azul vai ser o ângulo de deflexão θ 1 . da partícula 1 Pela imagem vemos que

    s e n θ 1 = b 2 a

    Como as partículas tem massas iguais podemos usar a seguinte relação θ 1 ' = 2 θ 1

    Para o disco de baixo então fica assim

    s e n θ 1 ' 2 = b 2 a

    θ 1 ' = 2 a r c s e n b 2 a  

    Pra achar o ângulo em relação ao CM do disco de cima usamos a seguinte relação θ 1 ' + θ 2 ' = π

    θ 2 ' = π - 2 a r c s e n b 2 a  

    Passo 2

  2. Galera, pela conservação da energia cinética temos que

P 1 f 2 2 m 1 + P 2 f 2 2 m 2 = P 2 i 2 2 m 2

Mas como as massas são iguas então podemos simplesmente escrever

P 1 f 2 + P 2 f 2 = P 2 i 2

Vamos olhar pros momentos lineares vetorialmente agora,

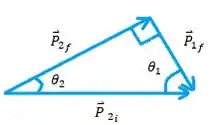
Pra que aquela relação de soma dos quadrados dos momentos lineares seja satisfeita, aquele ângulo de cima só pode ser de 90 ° , o que facilita bastante as coisas já que podemos escrever

  • Para o disco de cima

    • P 2 f = P 2 i s e n θ 1

    v 2 f = v 2 i s e n θ 1

    = v 2 i b 2 a

    A direção do vetor velocidade é dada por θ 2 = θ 2 ' 2

    θ 2 = π 2 - a r c s e n b 2 a  

  • Já para a velocidade do disco de baixo temos

v 1 f = v 2 i c o s θ 1

= v 2 i 1 - b 2 4 a 2

Resposta

a )   θ 1 ' = 2 a r c s e n b 2 a   e   θ 2 ' = π - 2 a r c s e n b 2 a  

b )   v 2 f = v 2 i b 2 a ;   θ 2 = π 2 - a r c s e n b 2 a

v 1 f = v 2 i 1 - b 2 4 a 2   ; θ 1 = a r c s e n b 2 a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bala de 4,00 g é disparada horizontalmente com velocidade de 400 m/s contra um bloco de madeira de 0,800 kg, inicialmente em repouso sobre uma superfície horizontal. A balaatravessa o bloco e emer
Um disco de hóquei azul de massa 0 , 0400 kg , deslizandocom velocidade igual a 0 , 200 m /s sobre uma mesa de ar horizontalsem atrito , sofre uma colisão frontal perfeitamente elástica com umdisco de
Suponha que você mantenha uma bola pequena em contato com uma bola grande diretamente sobre seu centro. Se você largar a bola pequena um pequeno intervalo de tempo após largar a bola grande, a bola pe
Uma bala ricocheteando. Uma pedra de 0,100 kg está em repouso sobre uma superfície horizontal sem atrito. Uma bala de 6,00 g, se deslocando horizontalmente a 350 m/s, colide com a pedra e ricocheteia
Um nêutron de massa m colide frontalmente com um núcleo de massa M, que está inicialmente em repouso. a) Mostre que se a energia cinética inicial do nêutron era de K0, a energia cinética que ele perde