Enunciado
Física - Young and Freedman - Vol 1- Ed: 10º - Capítulo 8.Problemas - Ex. 69
Uma bala ricocheteando. Uma pedra de 0,100 kg está em repouso sobre uma superfície horizontal sem atrito. Uma bala de 6,00 g, se deslocando horizontalmente a 350 m/s, colide com a pedra e ricocheteia ao longo da superfície com velocidade de 250 m/s em uma direção ortogonal à sua velocidade inicial. a)Determine o módulo, a direção e o sentido da velocidade da pedra após o impacto b) A colisão é perfeitamente elástica?
Passo 1
Beleza pessoal?! Espero que esteja tudo bem com meu os herdeiros de Newton. Vamos dar início a mais uma resolução com o padrão de qualidade do Responde aí, então pegue seu lápis, caderno e café e vamos nessa!!!
A massa da pedra é mA=0,100 kg e a massa da bala é mB=0,006 kg.
Seja +x na direção original da bala e +y em sua direção após a colisão com a pedra.
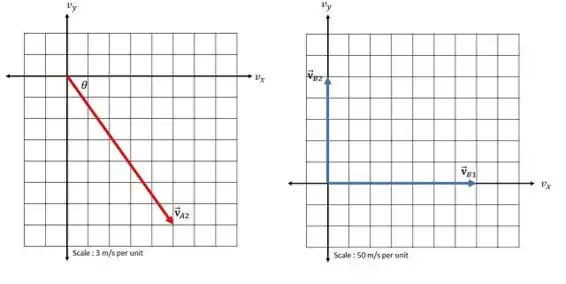
Portanto, a velocidade da bala antes da colisão é v⃗B1=(350 m/s) î e sua velocidade após a colisão é v⃗B2=(250 m/s) ĵ.
Sabemos que, em colisões de todos os tipos, uma vez que não há força resultante externa no sistema, o momento total antes da colisão é igual ao momento total após a colisão:
Se a colisão for entre duas partículas (A e B), então obtemos:
Assim, podemos escrever a equação de colisão da seguinte forma:
Também sabemos que, na colisão elástica entre duas partículas, as velocidades relativas antes e depois da colisão têm a mesma magnitude, mas sinais opostos; Então:
Passo 2
(a) Como a pedra está sobre uma superfície horizontal sem atrito, não há força horizontal externa no sistema; então os componentes do momento total do sistema são conservados separadamente.
Assim, para o componente −x:
Agora, temos os componentes da velocidade da pedra após a colisão, então obtemos sua magnitude da seguinte forma:
Passo 3
b) Para o lado esquerdo:
para o lado direito:
Desde v⃗A1−v⃗B1≠v⃗B2−v⃗A2v, então a colisão é inelástica.
Resposta
Ver o desenvolvimento