Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Problemas - Ex. 53

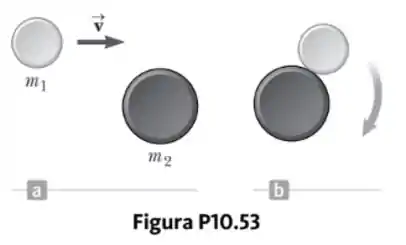
Um disco de massa m 1   =   80,0   g e raio r 1   =   4,00   c m desliza por uma mesa de ar com velocidade v   =   1,50   m / s , como mostrado na Figura P10.53a. Ele faz uma colisão oblíqua com um segundo disco de raio r 2   =   6,00   c m e massa m 2   =   120   g (inicialmente em repouso), de forma que suas bordas apenas se toquem. Como suas bordas são revestidas com uma cola de ação instantânea, os discos ficam grudados e giram após a colisão (Fig. P10.53b).

  1. Qual é o momento angular do sistema em relação ao centro de massa?
  2. Qual é a velocidade angular ao redor do centro de massa?

Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

Quando eles se tocam, o centro de massa está distante do centro do disco maior por:

y C M = 0 + 80.0 g 4.00 c m + 6.00 c m 120 g + 80.0 g = 4.00 c m

Letra a:

L = r 1 m 1 v 1 + r 2 m 2 v 2 = 0 + 6.00 × 10 - 2 m 80.0 × 10 - 3 k g ( 1.50 m / s ) = 7.20 × 10 - 3 k g ⋅ m 2 s

Passo 2

Letra b:

O momento de inércia sobre o CM é:

I = 1 2 m 1 r 1 2 + m 1 d 1 2 + 1 2 m 2 r 2 2 + m 2 d 2 2

I = 1 2 0.120 k g 6.00 × 10 - 2 m 2 + 0.120 k g 4.00 × 10 - 2 2 + 1 2 80.0 × 10 - 3 k g 4.00 × 10 - 2 m 2 + 80.0 × 10 - 3 k g 6.00 × 10 - 2 m 2

I = 7.60 × 10 - 4 k g ⋅ m 2

O momento angular do sistema de dois discos é conservado:

L = I ω ω = L I = 7.20 × 10 - 3 k g ⋅ m 2 s 7.60 × 10 - 4 k g ⋅ m 2 = 9.47 r a d / s

Resposta

  1. 7.20 × 10 - 3 k g ⋅ m 2 s
  2. 9.47 r a d s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma esfera maciça com 36,0N de peso sobe rolando um plano inclinado com um ângulo de 30,0 ° . Na base do plano inclinado, o centro de massa da esfera possui uma velocidade de translação de 4,90m / s .
Uma barra fina e homogênea com 0,5 m de comprimento e 4 k g de massa pode girar em um plano horizontal em torno de um eixo vertical que passa pelo centro da barra. A barra está em repouso quando uma b
Uma bolinha de massa de modelar, de massa m , cai do teto sobre a borda de uma plataforma giratória de raio R e momento de inércia I o que gira livremente com uma rapidez angular ω 0 em torno do seu e
Suponha que, na figura, l = 0,60 m , L = 2,0 m , M = 0,80 k g e m = 0,40 k g . O fio se rompe quando a rapidez angular do sistema se aproxima de um valor crítico ω i , ao mesmo tempo que a tensão no f
Uma barra uniforme, de massa M e comprimento L , está sobre uma mesa horizontal sem atrito. Uma bolinha de massa de modelar, de massa m = M / 4 , move-se ao longo de uma linha perpendicular à barra. D