Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 26.1 - Ex. 63
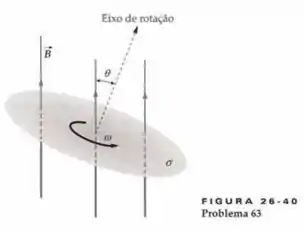
Um disco uniforme, fino, uniformemente carregado, de massa , raio e densidade superficial uniforme de carga , gira com rapidez angular em torno de um eixo que passa pelo seu centro e é perpendicular ao disco . O disco está em uma região com um campo magnético uniforme que faz um ângulo com o eixo de rotação. Calcule
a magnitude do torque exercido no disco pelo campo magnético
a frequência de precessão do disco no campo magnético.
Passo 1
E aí bonit@s, como vocês estão? Prontos pra mais uma questão bacana?
Se liga só, vamos chegar já atacando nossa questão direto aqui. Primeiramente devemos nos lembrar que a magnitude do torque que atua no disco é
Como a gente não é beste e nem nada, a forma como é dado para esse caso foi mostrada pra gente no livro e é expressa como
Substituindo em vamos encontrar
Pronto, tá resolvido nosso item.
Passo 2
Se você achou o item anterior tranquilo, se liga só nesse aqui. Se você observar bem, temos que a frequência de precessão é dada por
Onde para um disco sólido temos que o momento de inércia é dado por
Sendo assim, substituindo todos os dados vamos encontrar
E olha só, adivinha? Acabou mais uma questãozinha bem tranquila.