Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 26.1 - Ex. 75

Considere que os trilhos do problema 74 não tenham atrito, mas estejam inclinados, fazendo um ângulo θ com a horizontal, e que a fonte de corrente esteja conectada à extremidade mais baixa dos trilhos. O campo magnético ainda está dirigido verticalmente para baixo.

( a ) Qual o valor mínimo de B necessário para evitar que a barra deslize para baixo nos trilhos?

( b ) Qual é a aceleração da barra se B é o dobro do valor encontrado na parte ( a ) ?

Passo 1

E aí meus consagrados, como vocês estão?

Pois bem, meus camaradas observem que, com os trilhos inclinados, F → ainda aponta horizontalmente para a direita ( I , e portanto l → , estão fora da página). Para esse problema vamos escolher um sistema de coordenadas em que a inclinação seja na direção + x . Em seguida, podemos aplicar uma condição de equilíbrio translacional para encontrar o campo magnético vertical B → necessário para evitar que a barra deslize pelos trilhos. Na Parte ( b ) , podemos aplicar a segunda lei de Newton para encontrar a aceleração da barra transversal quando B é o dobro do seu valor encontrado em ( a ) . Esquematizando o problema teremos mais ou menos o seguinte

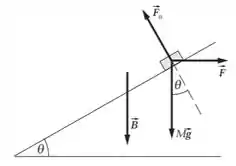
Passo 2

Aplicando as condições de equilíbrio para o eixo x (indicando a quase iminência do movimento) vamos ter

∑ F x = 0 → m ⋅ g ⋅ s i n θ - I ⋅ l ⋅ B ⋅ cos ⁡ θ = 0

Isolando B encontraremos

B = m g I l ⋅ tan ⁡ θ ,   o n d e   B → = - m g I l ⋅ tan ⁡ θ   û v

Onde û v é o vetor diretor unitário.

Passo 3

Para o segundo item vamos aplicar a segunda lei de Newton da seguinte forma

I l B ' ⋅ cos ⁡ θ - m g ⋅ s i n θ = m a

Resolvendo para a encontramos

a = I l B ' m ⋅ cos ⁡ θ - g ⋅ sin ⁡ θ

Se B ' = 2 B então a aceleração da barra será

a = 2 I l ⋅ m g I l ⋅ tan ⁡ θ m ⋅ cos ⁡ θ - g ⋅ sin ⁡ θ

a = 2 g ⋅ sin ⁡ θ - g ⋅ sin ⁡ θ = g ⋅ sin ⁡ θ

Reparem que a direção da aceleração é subindo com a inclinação. Prontinho, tá resolvido mais um probleminha bacana.

Resposta

a B → = - m g I l ⋅ tan ⁡ θ   û v

b   a = g ⋅ sin ⁡ θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um fio de 1,80 m de comprimento é percorrido por uma corrente de 13,0 A e faz um ângulo de 35,0 º º com um campo magnético uniforme de módulo B = 1,50 T . Calcule a força magnética exercida pelo campo
A Fig. 28-48 mostra um anel circular de fio com um raio a = 1,8 c m , submetido a um campo magnético divergente de simetria radial. O campo magnético em todos os pontos do anel tem o mesmo módulo B =
Na Fig. 28-46, um fio metálico de massa m = 24,1 m g pode deslizar com atrito insignificante sobre dois trilhos paralelos horizontais separados por uma distância d = 2,56 c m . O conjunto está em uma
O fio dobrado da Fig. 28-45 está submetido a um campo magnético uniforme. Cada trecho retilíneo tem 2,0 m de comprimento e faz um ângulo θ = 60 ° com o eixo x . O fio é percorrido por uma corrente de
Uma linha de transmissão horizontal é percorrida por uma corrente de 5000 A no sentido sul-norte. O campo magnético da Terra ( 60,0 μ T ) tem a direção norte e faz um ângulo de 70,0 ° com a horizontal