Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 117
Um disco uniforme de raio e massa gira em torno de um eixo horizontal paralelo ao seu eixo de simetria e que passa por um ponto de seu perímetro, de forma a poder oscilar livremente em um plano vertical. Ele é largado do repouso, com seu centro de massa à mesma altura do pivô. (a) Qual é a rapidez angular do disco, quando seu centro de massa está diretamente abaixo do pivô? (b) Qual é a força exercida pelo pivô sobre o disco neste momento?
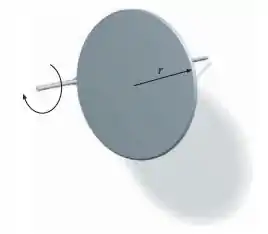
Passo 1
a) Oláaa, querido! Cê tá bem?
Então, ele quer a rapidez de um disco quando está no ponto mais baixo da sua trajetória. Sendo que o eixo de rotação está na borda do disco.
Nessa situação, com a rotação do disco ao redor do eixo, as energias potencial gravitacional e cinética rotacional ficam variando, de forma que convertem-se uma na outra. Então vamos usar a conservação de energia para achar no ponto mais baixo como ele pede.
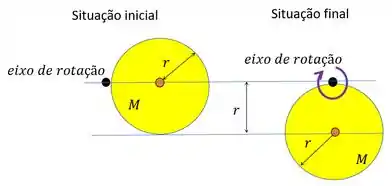
Quando o disco está na altura do pivô, não há rapidez angular , porque ele está em repouso. Só temos energia potencial. E vai ser a diferença de altura entre o centro do nosso disco e o centro do disco na situação final. Ou seja, . Por isso, temos
Já no ponto mais baixo, não temos energia potencial, já que . Mas temos enegia cinética de rotação, pois agora temos rapidez angular. Então
Assim a conservação de energia fica:
Passo 2
Mas se liga, a gente conhece o momento de inércia do disco quando o eixo passa pelo seu centro (centro de massa). Nessa situação isso não acontece. A gente tem que usar o que então? Isso aí, teorema dos eixos paralelos! Ele diz que
O momento de inércia de um disco em relação a um eixo que passa pelo centro de massa dele é . Subsituindo:
Cara, é a distância entre o centro de massa do disco e o eixo de rotação do nosso caso. Como o eixo de rotação está na borda do nosso disco, . Substituindo:
Colocando isso lá na equação de conservação:
Isolando quem a gente quer
Passo 3
(b) Queremos saber a força que o eixo faz no disco quando ele está na posição mais baixa:
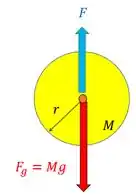
Então, o nosso disco faz um movimento circular em torno do eixo de rotação, certo? Logo, a força resultante na direção vertical vai ter um papel de força centrípeta, que ponta para o eixo de rotação (para cima). Assim a gente pode escrever que
Nessa situação, o pivô puxa o disco para cima com uma força , enquanto o peso faz força para baixo.
Passo 4
Só que a força centrípeta é dada por
E temos que :
Substituindo isso na nossa equação :
Substituindo o valor de que a gente tinha achado e isolando :