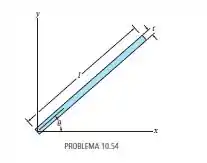
Determine o produto de inércia da fina faixa de área em relação aos eixos e . A faixa é orientada a um ângulo em relação ao eixo . Considere que .
Passo 1
E aí! tudo certinho?
Nesse problema temos que calcular o produto de inércia da faixa em relação a e .
Parece complicado?
Para resolver esse problema temos que lembrar que o produto de inércia em e é dada por:
Bora lá!
Passo 2
Foi dito no enunciado que , assim, podemos dizer:
Com
Assim, reescrevendo a integral que vimos no passo 1, temos:
Como e são constantes...
Podemos ainda aplicar a identidade trigonométrica:
Assim, ficando:
E aí! o que achou? Responde Aí!