Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 124
Um cordão é enrolado em torno de um cilindro maciço e homogêneo, de raio e massa , que está colocado sobre uma superfície horizontal sem atrito. (O cordão não toca a superfície, porque existe uma ranhura na superfície, dando espaço ao cordão.) O cordão é puxado horizontalmente, de cima, com uma força . (a) Mostre que a magnitude da aceleração angular do cilindro é duas vezes a magnitude da aceleração angular necessária para o rolamente sem deslizamento, de forma que o ponto mais baixo do cilindro desliza para trás, em relação à mesa. (b) Determine a magnitude e o sentido da força de atrito, em ter a mesa e o cilindro, que seriam necessários para o cilindro rolar sem deslizar. Qual seria a magnitude da aceleração do cilindro, neste caso?
Passo 1
Essa aí é bem parecida com várias que já fizemos, né? É o de sempre, vamos analisar as forças em cada direção, a rotação, e pronto, fechou! O desenho das forças vai ficar assim:
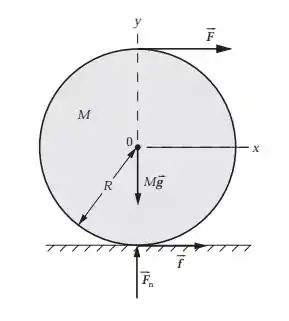
Passo 2
- Da segunda lei de Newton para a rotação, considerando o centro de massa do cilindro:
- Se considerarmos o ponto de contato com o chão como o pivô, o torque nesse ponto é:
Mas a aceleração do centro de massa pode ser calculada também:
Como sabemos da rotação sem deslizamento, , para o ponto de contato.
Passo 3
Pra calcular o momento de inércia do cilinro com relação ao pivô, vamos usar o teorema dos eixos paralelos:
Substituindo aí em cima:
E como ,
Na segunda lei de Newton para o cilindro:
Essa força atua no mesmo sentido de , ou seja, no eixo positivo.
Resposta
- , no sentido positivo.