Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.2 - Ex. 2
A distância entre os eixos dianteiro e traseiro de um automóvel é . A massa do automóvel é e o centro de gravidade está situado atrás do eixo dianteiro. Com o automóvel em terreno plano, determine o módulo da força exercida pelo solo :(a) Sobre cada roda dianteira (supondo que as forças exercidas sobre as rodas dianteiras são iguais) (b) sobre cada roda traseira (supondo que as forças exercidas sobre as rodas traseiras são iguais).
Passo 1
(a)Primeiro, a gente precisa observar quais são as forças exercidas sobre o automóvel. Para isso, vamos usar a Figura abaixo
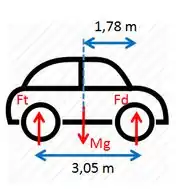
tal que , e são as forças exercidas pelo solo sobre as rodas traseiras, sobre as dianteiras e a peso.
Passo 2
Agora, vamos relacionar essas forças. Na vertical, o carro não é acelerado, então, essas forças se equilibram assim:
Passo 3
O próximo passo agora é usar outra relação entre essas forças através do equilíbrio de torques. Fazendo o equilíbrio de torques com relação à roda dianteira, temos:
Passo 4
Temos agora um sistema com duas equações (encontradas nos passos 3 e 2) e duas variáveis e . Então, podemos encontrar a solução! Substituindo o valor de na penúltima equação, temos:
Passo 5
Aqui é importante ter atenção! A força encontrada acima é exercida sobre as duas rodas dianteiras. Para acharmos a intensidade da força que o solo exerce sobre cada uma delas, temos que dividi-la por dois:
Passo 6
(b)Pronto, agora só temos que usar a última equação do passo 3:
Passo 7
Novamente, esse resultado é a força que o solo exerce sobre as duas rodas. Finalmente, vamos dividi-la por dois e obter o quanto de força o solo exerce sobre somente uma roda traseira:
Resposta
(a)
(b)