Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 16.7 - Ex. 49
Uma corda de violão de náilon tem uma massa específica linear de e está sujeita a uma tensão de . Os suportes fixos estão separados por uma distância . A corda está oscilando da forma mostrada na figura. Calcule (a) a velocidade, (b) o comprimento de onda e (c) a frequência das ondas progressivas cuja superposição produz a onda estacionária.
Passo 1
Show de bolinhas pessoal, nesse exercício aqui o enunciado nos deu que uma corda de violão de náilon, tem uma massa especifica de e está sujeita a uma tensão de . Sabendo que os suportes fixos estão separados por uma distância , na letra (a), o enunciado nos pede pra calcular o valor da velocidade.
Iradoso, pra isso vamos precisar lembrar da equação que relaciona a velocidade de propagação da onda em uma corda com a tensão à qual ela é submetida e com sua velocidade linear. A relação entre essas grandezas é essa daqui:
Onde e são a tensão e a densidade linear da corda.
Belezoca, então substituindo os valores que o enunciado nos deu, e , vamos obter que:
Logo:
Passo 2
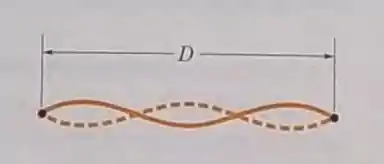
Belejóia, o próximo passo agora é identificar a qual harmônico corresponde a oscilação da corda mostrada na figura. Olhando a figura que o enunciado nos deu, a gente consegue perceber que:
Pois é a distância entre dois nós consecutivos.
Então, podemos encontrar isolando ele na equação, tal que:
Como , vamos obter que o comprimento de onda será:
Passo 3
Finalmente, na letra (c), como queremos a frequência das ondas progressivas que produzem onda estacionária, a gente pode aplicar a relação entre velocidade, comprimento de onda e velocidade:
Sendo assim:
E se a gente substituir os valores, vamos descobrir que: