Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.Problemas Adicionais - Ex. 79

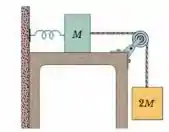
Dois blocos, de massas M   =   2,0   k g e 2 M , estão presos a uma mola de constante elástica k   =   200   N / m que tem uma das extremidades fixa, como mostra a Fig. 8-67. A superfície horizontal e a polia não possuem atrito e a polia tem massa desprezível. Os blocos são liberados a partir do repouso com a mola na posição relaxada. (a) Qual é a energia cinética total dos dois blocos após o bloco que está pendurado ter descido 0,090   m ? (b) Qual é a energia cinética do bloco que está pendurado depois de descer 0,090   m ? (c) Qual é a distância que o bloco pendurado percorre antes de parar momentaneamente pela primeira vez?

Passo 1

  1. Oi, pessoal! Tudo bom? A primeira coisa que devemos fazer é definir as condições iniciais do problema.

    2. Vamos tomar como referência para a energia potencial a altura inicial do bloco 2 M . Quando o bloco 2 M começa a descer, a energia potencial total é a soma da energia potencial gravitacional com a energia potencial elástica da mola. Nós temos que a energia cinética total, por sua vez, é a soma das energias cinéticas dos dois blocos.

    Sendo assim , temos que :

    K i   +   U i   =   K t o t   +   U t o t  

    Como o sistema parte do repouso e equilíbrio, as energias cinética e potencial inicial são zeros,

      0   +   0   =   K t o t   +   U t o t

    Como temos energia potencia da mola envolvida, temos

    0 = K t o t + m g y + 1 2 k x 2

    Substituindo os dados do enunciado para M = 2,9   k g

      0 = K t o t +   2 2,0 9,8 – 0,090 + 1 2   200 0,090 2

    K t o t   =   2,7   J

    Passo 2

  2. Bom pessoal, nós temos que a energia cinética do bloco 2 M constitui uma fração conhecida da energia cinética total:

    3. K 2 M K T O T = 2 M v 2 2 3 M v 2 2 = 2 3

    Dessa forma, a energia cinética do bloco que está pendurado é dada por :

    K 2 M   = 2 3 ( 2,7   J )   =   1,8   J

    Passo 3

  3. Bom galera , para resolvermos este item, basta fazer y   =   – d   ,     K t o t   =   0 e calcular o valor de d . Sendo assim , temos que :

K i + U i = K t o t + U t o t

0 + 0 = 0 + 2 M g - d + 1 2 k d 2

Para M   =   2,0   k g , obtemos,

d   =   0,39   m

Resposta

  1. K t o t = 2,7 J
  2. K 2 M = 1,8 J
  3. d = 0,39   m

Tranquilo galera?? Bora resolver mais questões então

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um projétil é lançado da borda de um penhasco com uma energia cinética inicial de 1550J . A maior distância vertical para cima que o projétil atinge em relação ao ponto de lançamento é + 140m . Qual é
Uma partícula A e uma partícula B são empurradas uma contra a outra, comprimindo uma mola colocada entre as duas. Quando as partículas são liberadas, a mola as arremessa em sentidos opostos. A massa d
(a)No Problema 7, qual é a velocidade da bola no ponto mais baixo? (b) Essa velocidade aumenta, diminui ou permanece a mesma se a massa aumenta?
(a)No Problema 8, usando técnicas de energia em vez das técnicas do Capítulo 4, determine a velocidade da bola de neve ao chegar ao solo. Qual seria essa velocidade (b) se o ângulo de lançamento fosse
No Problema 6, qual é o módulo da componente (a) horizontal e (b) vertical da força resultante que atua sobre o bloco no ponto Q ? (c) De que altura h o bloco deveria ser liberado, a partir do repouso