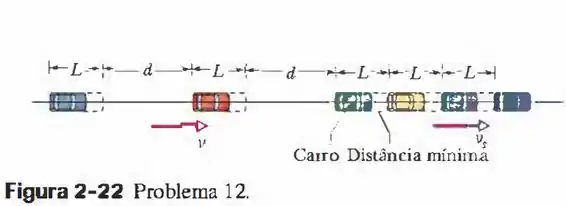
Onda de choque no trânsito. Quando o trânsito é intenso, uma redução brusca de velocidade pode se propagar como um pulso, denominado onda de choque, ao longo da fila de carros. A onda de choque pode ter o sentido do movimento dos carros, o sentido oposto ou permanecer estacionária. A Fig mostra uma fila de carros regularmente espaçados que estão se movendo a uma velocidade em direção a uma fila de carros mais lentos, uniformemente espaçados, que estão se movendo a uma velocidade . Suponha que cada carro mais rápido acrescenta um comprimento ( comprimento do carro mais a distância mínima de segurança) à fila de carros mais lentos ao se juntar à fila, e suponha que reduz bruscamente a velocidade no último momento. (a) Para que distância d entre os carros mais rápidos a onda de choque permanece estacionária? Se a distância é duas vezes maior que este valor, quais são (b) a velocidade e (c) o sentido (o sentido do movimento dos carros ou o sentido contrário) da onda de choque?

Iradoso, agora como sabemos a velocidade do carro e o tempo que ele deve demorar para percorre uma distância podemos descobrir , tal que:

Portanto:

Show de bolinhas, então sendo duas vezes maior, os carros estacionados percorrem uma distância , enquanto o carro rápido percorre uma distância , sendo assim:

Logo:

Então isolando a distância :

Sendo assim, obtemos que:

Sabendo que ,podemos encontrar de forma que:

A velocidade da onda de choque é zero quando , é positiva quando e negativa quando e a velocidade é dada por:

Logo:

Como , a onda de choque é no sentido positivo (sentido do movimento dos carros).