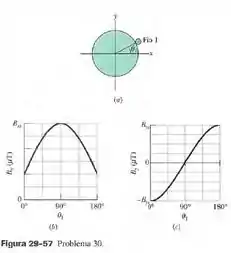
Dois fios longos retilíneos percorridos por corrente estão apoiados na superfície de um cilindro longo de plástico de raio , paralelamente ao eixo do cilindro. A figura 29-57a mostra, em seção reta, o cilindro e o fio 1, mas não o fio 2. Com o fio 2 mantido fixo no lugar, o fio 1 é deslocado sobre o cilindro, do ângulo até o ângulo , passando pelo primeiro e segundo quadrantes do sistemade coordenadas xy. O campo magnético no centro do cilindro é medido em função de . A figura 29-57b mostra a componente de em função de (a escalavertical é definida por ea figura 29-57c mostra a componente em função de (a escala vertical é definida por ). (a) Qual é o ângulo que define a posição do fio 2? Determine (b) 0 valor e (c) o sentido (para dentro ou para fora do papel) da corrente no fio 1. Determine também (d) o valor e (e) o sentido da corrente no fio 2.

De acordo com o gráfico da figura 29-57b, quando a componente x do campo magnético produzido pelo fio 1 é zero (o que, de acordo com a regra da mão direita, acontece quando o ângulo que o fio 1 faz com o eixo x é ), a componente x do campo magnético total é , e quando a componente x do campo magnético produzido pelo fio 1 é máxima (o que, de acordo com a regra da mão direita, acontece quando o ângulo que o fio 1 faz com o eixo x é a componente total do campo magnético total é . Isso significa que , o que, de acordo com a equação do campo para fios longos nos dá:

Podemos ver que na figura 29-57b, aumenta quando varia de até , o que nos leva a concluir que o sentido da correntne no fio 1 é para fora do papel.

A componente x do campo produido pelo fio 2 é Assim, de acordo com a equação do campo para fios longos:

E, de acordo com a regra da mão direita, o sentido da corrente no fio 2 é para dentro do papel.