Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.2 - Ex. 16
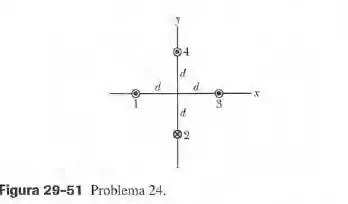
A figura 29-51 mostra, em seção reta, quatro fios finos paralelos, retilíneos e muito compridos, que conduzem correntes iguais nos sentidos indicados. Inicialmente, os quatro fios estão a uma distância da origem do sistema de coordenadas, onde criam um campo magnético total . (a) Para que valor de o fio 1 deve ser deslocado ao longo do eixo para que o campo sofre uma rotação de no sentido anti-horário? (b) Com o fio 1 na nova posição, para que valor de o fio 3 deve ser deslocado ao longo do eixo para que o campo volte à orientação inicial?
Passo 1
Inicialmente, e . Para obter a rotação de descrita ao enunciado, devemos ter:
na qual e . Como , isso nos dá:
Passo 2
Para , obtemos . Olhando a geometria do problema, concluímos que é preciso deslocar os fio 1 para .
Passo 3
Para que o campo volte à orientação inicial, basta restabelecer a simetria inicial, deslocando o fio 3 para .
Resposta
- ;
- .