Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.2 - Ex. 30
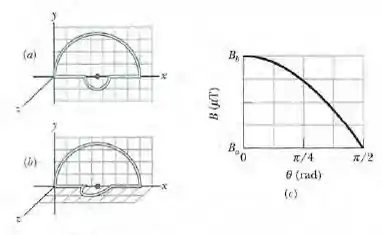
A espira percorrida por corrente da figura 29-58a é constituída por uma semicircunferência com de raio, uma semicircunferência menor com o mesmo centro e dois seguimentos radiais, todos no mesmo plano. A semicircunferência menor sofre uma rotação de um ângulo para fora do plano (figura 29-58b). A figura 29-58c mostra o módulo do campo magnético no centro de curvatura em função do ângulo . A escala vertical é definida por e . Qual é o raio do semicírculo menor?
Passo 1
Fala aí, galerinha! 😎
Nesse problema temos uma espira percorrida por uma corrente e é constituída por uma semicircunferência com de raio, uma semicircunferência menor com o mesmo centro e dois seguimentos radiais, todos no mesmo plano.
A semicircunferência menor sofre uma rotação de um ângulo para fora do plano. A figura 29-58c mostra o módulo do campo magnético no centro de curvatura em função do ângulo . A escala vertical é definida por e e a partir daí queremos saber qual é o raio do semicírculo menor?
Tem ideia de como fazer isso? 🤔
De acordo com a equação do campo para um semicírculo, o campo inicial é:
Quando a espira menor está na posição final, o teorema de pitágoras nos dá:
Veja só! 😊
Passo 2
Elevando ao quadrado e dividindo por , obtemos:
na qual . Observando o gráfico da figura 29-59c, chegamos à conclusão de que , o que nos dá:
Como sabemos que , a únida resposta aceitável é .
E aí! entendeu tudo? Responde Aí! 😁
Resposta
O raio do menor semicírculo é: