Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 3- Ed: 1º - Capítulo 3.Problemas - Ex. 5

Dois fios retilíneos de mesmo comprimento a , separados por uma distância b , estão uniformemente carregados com densidade lineares de carga λ e - λ (fig.) Calcule o campo elétrico no centro P do retângulo de lados a e b .

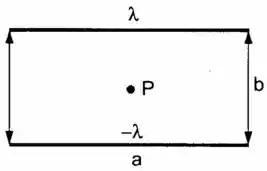
Passo 1

Se liga! Vamos começar calculando primeiro o campo produzido pelo fio superior, beleza?

Olha a figura!

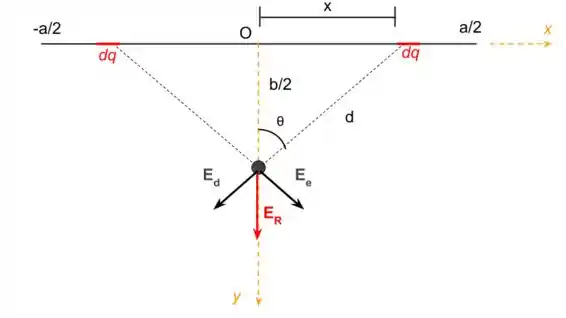
Lembre-se que podemos escrever

λ = d q d l   ⟹ d q = λ   d l e que pela figura podemos escrever que

d l = d x  

Passo 2

Podemos notar na figura que os campos produzidos pelo elemento infinitesimal do lado esquerdo ( E e →   ) e o gerado pelo elemento do lado direito ( E d →   ) ao se somarem, as componentes que apontam no eixo x se anulam. Sendo assim, teremos apenas as componentes no eixo y .

Lembre-se que o campo produzido por um elemento infinitesimal pode ser escrito como

d E = k d q d 2 =   k λ d x d 2

Podemos escrever que

d = x 2 + b 2 2

Levando em consideração que só teremos campo na direção y , temos que

d E = k d q d 2 =   k λ d x x 2 + b 2 2 c o s θ

Onde

c o s θ = b / 2 x 2 + b 2 2

Assim podemos reescrever a expressão do campo d E como

d E = k 2 λ d x   b x 2 + b 2 2 3 / 2

Passo 3

Para achar o campo produzido pelo fio inteiro, basta integrarmos d E

Pela imagem podemos verificar que x vai variar de - a /2 até a / 2 . Sendo assim, o campo do fio produzido pelo fio fica

E = k λ b 2 ∫ - a / 2 a / 2   d x x 2 + b 2 2 3 / 2 =   k λ b 2 ∫ - a / 2 a / 2   8 d x 2 x 2 + b 2 3 / 2   Agora precisamos resolver a integral, certo?! Essa integral é tabelada! Pela tabela temos

∫ d u a 2 + u 2 3 / 2 =   u a 2 a 2 + u 2 + C

Sendo assim, empregando os intervalos de integração teremos E = 8 k λ b 2 1 2 a b 2 a 2 + b 2 -   - a b 2 a 2 + b 2 =   8 k λ b 4 b 2 2 a a 2 + b 2

Substituindo

k = 1 4 π ϵ o

Temos

E =   λ π ϵ 0 b a a 2 + b 2

E ele aponta no sentido positivo de y . Portanto

E → =   λ π ϵ 0 b a a 2 + b 2     y ^

Passo 4

Por simetria, o campo produzido pelo fio inferior, será de mesma magnitude que o produzido pelo superior. Cabe ressaltar que como no fio inferior a densidade linear de carga é - λ , o campo deve apontar na direção positiva de y .

Portanto no ponto P, os campos produzidos pelo fio será E → T o t a l = 2   E → =   =   2 λ π ϵ 0 b a a 2 + b 2     y ^

Resposta

E → T o t a l = 2   E → =   =   2 λ π ϵ 0 b a a 2 + b 2     y ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas linhas de carga infinitas, cada qual com uma densidade linear de carga, estão posicionadas ao longo dos eixos x e y, passando ambas pela origem. Qual é a intensidade do campo elétrico na posição
A FIGURA P27.36 é uma secção transversal de duas linhas de carga infinitas que se estendem perpendicularmente para fora da página. Ambas possuem a mesma densidade linear de carga λ . Obtenha uma expre
Três bastões com 10 cm de comprimento cada formam um triângulo equilátero sobre um plano. Dois deles estão carregados com + 10n C , e o terceiro, com - 10n C . Qual é a intensidade do campo elétrico n
Mostre que uma linha de carga infinita, com densidade linear de carga , exerce sobre um dipolo elétrico uma força atrativa de intensidade F = 2 λ p 4 π ϵ 0r 2 . Considere que r seja muito maior do que
O campo elétrico a 5,0 cm de um fio longo e carregado é ( 2000N C , ao longo do fio). Qual é a carga (em nC) de um segmento do fio com 1,0c m de comprimento?