No modelo clássico de J.J. Thomson para átomo de hidrogênio, a carga do núcleo era imaginada como sendo uniformemente distribuída no interior de uma esfera de raio da ordem de (raio atômico) e o elétron era tratado como uma partícula pontiforme movendo-se no interior desta distribuição.
- Calcule o campo elétrico que atuaria sobre o elétron num ponto à distância do centro da esfera;
- Mostre que o elétron poderia mover-se radialmente com um movimento harmônico simples;
- Calcule a frequência de oscilação e compare-a com uma frequência típica de luz visível, bem como com o resultado do problema 3 do capítulo 2
Passo 1
Se liga! Temos aqui um problema com simetria esferérica!
Pronto para usar a lei de Gauss?!
Vamos começar com o desenho do problema, blz?
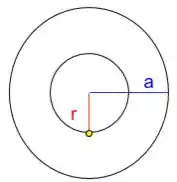
Ele pediu para calcular o campo na região .
A lei de Gauus noss diz que
Passo 2
Mas quem é a área?Vamos considerar que o elétron está representado no ponto amarelo. Sendo assim, a área da esfera de raio é
Passo 3
Agora vem a outra questão, quem é ?
Isso mesmo, é a carga localizada dentro da esfera de raio.
Como foi dito no enunciado, a carga total da esfera maior é . Agora precisamos achar a relação de com .
Temos que a densidade de carga volumétrica é
Substituindo e na expressão do fluxo para calcular o campo, teremos
Passo 4
Para provar que o elétron poderia realizar um MHS, precisamos achar a equação do movimento.
Sabemos que a força elétrica é
Substituindo a a carga do elétron e o campo, temos
Aplicando a lei de newton podemos escrever que
Agora podemos escrever a equação na forma do MHS
Passo 5
Sabemos que a equação do MHS geralmente é escrita da seguinte forma
Comparando com a expressão do MHS obtida, temos que
Substituindo por valores conhecidos temos
Para comparar com a frequência da luz, precisamos relacionar a frequência com