Dois fios retos, longos e paralelos conduzem correntes de intensidade em sentidos opostos, como mostra a Figura 22.17. A distância entre os fios é . (a) Calcule a expressão para o campo magnético gerado pelos dois fios ao longo do eixo , que cruza os dois fios de forma ortogonal. (b) Faça um gráfico de . Escolha a origem das coordenadas no ponto equidistante dos fios.

Passo 1
Eai pessoal, beleza?
Para resolver essa questão é bem importante que você conheça o campo produzido por um fio reto. Você deve ter visto nas primeiras seções do capítulo que o campo produzido por um fio longo e reto em que passa uma corrente é dado por
Nessa expressão, é a distância até o centro do fio. Esse resultado foi deduzido na seção 22.2 do livro.
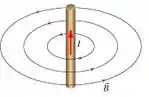
Vale ressaltar que esse campo “circula” em torno do fio respeitando a regra da mão direita:
Vamos olhar agora para a situação desse problema! A seguir eu represento as linhas de campo produzidas por cada fio:
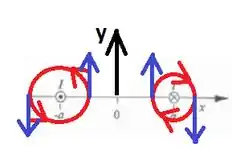
Observe que sobre o eixo as componentes dos campos estarão na direção .Para , o campo do fio da esquerda será
Já o do fio da direita será
Com isso, nessa região teremos
PS: um campo negativo indica que ele aponta na direção negativa do eixo .
Passo 2
Já para , temos
Assim,
Por fim, para , temos
Portanto,
Observe que os campos são iguais nas três regiões:
Ou ainda,
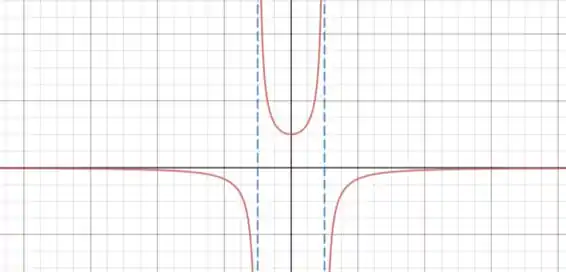
A seguir temos um esboço dessa função: