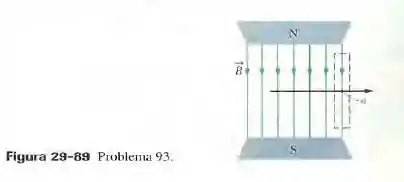
Mostre que um capo magnético uniforme B não pode diminuir bruscamentepara zero (como pode parecer pela falta de linhas de campo à direita do ponto na Fig. 29-89) quando nos deslocamos perpendicularmente a , ao longo, por exemplo, da seta horizontal da figura. (Sugestão: aplique a lei de Ampère à amperiana retangular indicada pelas retas tracejadas.) Nos imãs reais, o campo tende a zero gradualmente quando nos afastamos da região entre os polos. Modifique as linhas de campo da figura para torná-las mais realistas.

De acordo com a lei de Ampère,

Na qual é a corrente total envolvida pela amperiana. Para a trajetória tracejada na Figura 29-89, , já que a corrente que entra pelo llado de cima é igual à corrente que sai pel olado de baixo. A integral é zero no lado esquerdo, no lado de cima e no lado de baixo do percurso: no lado direito, porque o campo é zero; no lado de cima e no lado de baixo, porque o campo é perpendicular a Se é o comprimento do lado esquerdo, a integral completa é , na qual B é o módulo do campo do lado esquerdo da trajetória. Como são diferentes de zero, a lei de Ampère não é respeitada, pois o lado esquerdo é diferente de zero e o lado direito é igual a zero.

A causa da aparente contradição é o fato de que as linhas de campo magnético mostradas na figura 29-89 não estão correteas. Na verdade, as linhas de campo se encurvam para fora nas bordas da região onde existe campo magnético e a concentração das linhas diminui gradualmente, e não de forma abrupta, como na figura