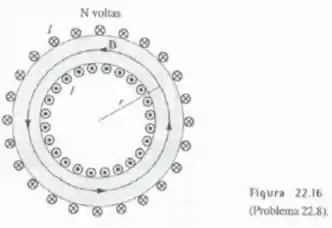
Campo de um toroide. Toroide é um corpo com forma de uma câmara de ar de pneu. Uma espira pode ser enrolada em torno do toroide, como mostra a Figura 22.16. Neste caso, conclui-se por análise de simetria que as linhas de força do campo magnético têm a forma de círculos fechados como mostra a figura. Calcule o campo magnético (a) no interior do toroide; (b) fora do toroide.

Eai pessoal, beleza?

Esse problema é o mais fácil do mundo se você lembrar qual é o campo dentro de um solenoide! Vimos na seção 22.6 do livro que o campo dentro de um solenoide é uniforme e dado por

onde é a corrente, é o número de espirar e é comprimento.

A gente pode pensar no toroide como sendo um solenoide em que entortamos as pontas até que elas se encontrem, fechando o toro! Com isso, o campo dentro do toroide será igual ao campo do solenoide, porém com

Assim,