Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 1.Problemas - Ex. 59
Dois operários puxam horizontalmente uma caixa pesada, mas um deles usa o dobro da força do outro. A maior tração está na direção 21,0º de norte para oeste, e o resultante dessas duas forças é 460,0 N no sentido norte. Use os componentes vetoriais para achar o módulo de cada uma dessas forças e a direção e o sentido da menor força
Passo 1
E aiii galera!
Tudo bom com vocês?
Vamos fazer mais uma questãozinha?
Bom... o enunciado nos diz que dois operários puxam horizontalmente uma caixa pesada, mas um deles usa o dobro da força do outro.
A maior tração está na direção de norte para oeste, e o resultante dessas duas forças é no sentido norte.
Queremos encontrar o módulo, a direção e o sentido da menor força.
Para isso, temos que desenhar os vetores no plano cartesiano e analisar suas componentes para encontrarmos o vetor que queremos.
Passo 2
Abaixo temos a seguinte figura para ilustração para o que o enunciado nos deu:
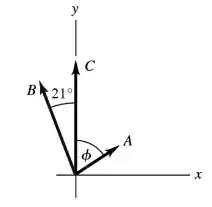
Seja:
E isso nos dá:
Passo 3
Na figura:
Nos dá:
A solução é que a tração menor seja a ao nordeste. Neste caso, a tração menor é e a tração maior é .
Passo 4
Também podemos fazer também da seguinte forma:
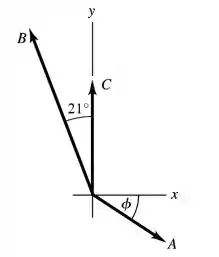
Onde, seguindo a mesma lógica, temos que .
Assim, temos:
A outra solução é que a tração menor seja a ao sudeste. Neste caso, a tração menor é e a maior é .
Resposta
A solução é que a tração menor seja a 45.8º ao nordeste. Neste caso, a tração menor é 179N e a tração maior é 393N.
A outra solução é que a tração menor seja a 45.8º ao sudeste. Neste caso, a tração menor é 393N e a maior é 786N.