Bob caminha 200 m para o sul, depois troteia 400 m para o sudoeste e finalmente caminha 200m na direção a leste de norte.
a. Trace uma representação gráfica acurada do movimento de Bob. Use régua e transferidor.
b. Use trigonometria ou os componentes para determinar o deslocamento com o qual Bob retornará ao ponto de partida pela rota mais direta possível. Expresse sua resposta como uma distância e uma orientação.
c. Sua resposta ao item anterior está em concordância com o que você mede em seu diagrama do item a?
Passo 1
- E aí galera, vamos representar
- Nos é dado , e pode usar trigonometria para obter e .
- O comprimento medido do vetor no gráfico (com uma régua) é aproximadamente vezes o valor medido comprimento do vetor . Dado que , isso dá . Da mesma forma, o ângulo medido com o transferidor é próximo de 60°. Essas respostas estão de acordo com a parte (b).
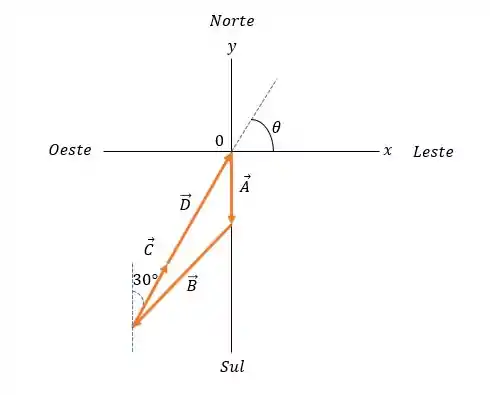
Nós conhecemos: , e queremos encontrar . Então vamos lá!
Observe que está ao leste e está ao norte.
Passo 2
Nós queremos . Isso quer dizer que:
A magnitude e direção de são:
e
Isso quer dizer que:
Passo 3
Resposta
-
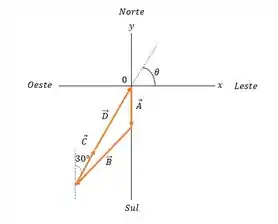
- Sim