Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 7.Exercícios e Problemas - Ex. 29

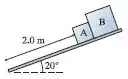
29. Dois pacotes dos Correios escorregam para baixo da rampa de 20 ° de inclinação mostrada na FIGURA P7.29. O pacote A tem uma massa de 5,0   k g e um coeficiente de atrito de 0,20 . O pacote B tem 10   k g de massa e coeficiente de atrito igual a 0,15 . Quanto tempo leva o caixote A para chegar à base da rampa?

Passo 1

Então galera para resolver esse problema temos de tomar os eixos x e y de forma diferente, o x paralelo a rampa e o eixo y perpendicular à rampa, assim nosso diagrama de corpo livre fica da seguinte maneira:

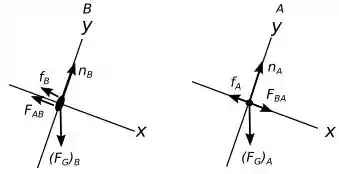
Tendo esse diagrama fica mais fácil de analisar o que temos. Olhe no diagrama que F A B = F B A , já que elas são um par de ação e reação do contrato entre os blocos.

Então para achar o tempo que o bloco A leva para chegar até o final da rampa vamos usar a seguinte equação da cinemática:

x 1 = x 0 + v 0 x t 1 - t 0 + 1 2 a t 1 - t 0 2

Bem dizer temos tudo o que precisamos dessa equação para encontrar t 1 só falta saber quem é a .

Essa aceleração a vai ser a aceleração na direção x tando do bloco A quanto de B . Para achá-la vamos usar a segunda lei de Newton na direção x para os dois blocos. A segunda lei nos diz que a soma das forças em uma dada direção é iguala a massa vezes a aceleração.

Passo 2

Vamos então analisar o bloco A , temos o seguinte:

m A a = F B A + F G A sen ⁡ θ - f A

⇒ m A a = F B A + m A g sen ⁡ θ - μ A n A

Como o bloco está em equilíbrio na direção y temos que:

n A = F G A = m A g cos ⁡ θ

Então temos que:

m A a = F B A + m A g sen ⁡ θ - μ A m A g cos ⁡ θ

⇒ F B A = m A a - m A g sen ⁡ θ + μ A m A g cos ⁡ θ

Passo 3

Vamos então agora analisar o bloco B , temos o seguinte:

m B a = - F A B + F G B sen ⁡ θ - f B

⇒ m B a = - F A B + m B g sen ⁡ θ - μ B n B

Como o bloco está em equilíbrio na direção y temos que:

n B = F G B = m B g cos ⁡ θ

Então temos que:

m B a = - F A B + m B g sen ⁡ θ - μ B m B g cos ⁡ θ

⇒ F A B = - m B a + m B g sen ⁡ θ - μ B m B g cos ⁡ θ

Passo 4

Agora usando o fato que pela terceira lei temos que:

F A B = F B A

Assim:

- m B a + m B g sen ⁡ θ - μ B m B g cos ⁡ θ = m A a - m A g sen ⁡ θ + μ A m A g cos ⁡ θ

Agora vamos isolar a , temos:

m A a + m B a = m B g sen ⁡ θ - μ B m B g cos ⁡ θ + m A g sen ⁡ θ - μ A m A g cos ⁡ θ

⇒ m A + m B a = m A + m B g sen ⁡ θ - μ A m A + μ B m B g co s ⁡ θ

⇒ a = g sen ⁡ θ - μ A m A + μ B m B g cos ⁡ θ m A + m B

Substituindo os valores que conhecemos, temos:

a = ( 9,8 ) sen ⁡ 20 ° - 0,2 5 + 0,15 10 ( 9,8 ) cos ⁡ 20 ° 5 + 10

= 3,35 - 23,02 15

Então temos que:

a = 1,82   m / s 2

Passo 5

Agora que temos a aceleração finalmente podemos encontrar o tempo que A leva para chegar na base da rampa, temos:

x 1 = x 0 + v 0 x t 1 - t 0 + 1 2 a t 1 - t 0 2

Substituindo o que sabemos, temos:

2 = 0 + 0 t 1 - 0 + 1 2 ( 1,82 ) t 1 - 0 2

⇒ 2 = 0,91 t 1 2

Então temos que:

t 1 = 1,48   s

Resposta

t 1 = 1,48   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

25 . || a . Por que um carro acelera, mas uma casa não pode fazê-lo? A explicação deve ser dada em termos das forças e de suas propriedades. b . Dois terços do peso de um carro de 1.500k g com motor d
17 . || Um móbile de um museu de arte tem um gato de aço de 2,0k g e um cachorro, também de aço e de 4,0k g , suspensos em um cabo sem massa, como mostra a F I G U R AE X 7.17 . Constata-se que θ 1 =2
22 . || Uma corda de 3,0m de comprimento e 2,2k g de massa é pendurada no telhado de uma casa. Desenhe o gráfico da tensão na corda em função da posição ao longo da corda, partindo da extremidade infe
Os Exercícios de 1 a 6 descrevem, cada um, uma situação. Em cada um:a. Seguindo os passos do Box Tático 7.1, desenhe um diagrama de interação.b. Identifique o “sistema” em seu diagrama de interação.c.
Os Exercícios de 1 a 6 descrevem, cada um, uma situação. Em cada um:a. Seguindo os passos do Box Tático 7.1, desenhe um diagrama de interação.b. Identifique o “sistema” em seu diagrama de interação.c.