Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 7.Exercícios e Problemas - Ex. 33

33. O coeficiente de atrito estático entre os dois blocos da FIGURA P7.33 vale 0,60 . O coeficiente de atrito cinético entre o bloco inferior e o piso é de 0,20 . A força F → faz com que os dois blocos percorram uma distância de 5,0   m , tendo partido do repouso. Qual é o mínimo intervalo de tempo no qual este movimento pode ser completado sem que o bloco superior escorregue sobre o inferior?

Passo 1

Então pessoal a base que precisamos para resolver esse problema é a segunda e a terceira lei de Newton, mas para sabermos como usá-las bem, vamos montar um diagrama de corpo livre para cada bloco do nosso sistema, temos o seguinte:

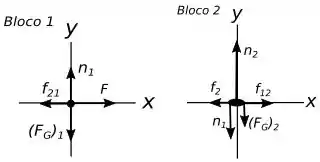
Vamos nos referir ao bloco de cima como bloco 1 e o de baixo como bloco 2 .

Agora vamos analisar a nossa situação junto com o diagrama para ver os pares de ação e reação que temos presentes.

Temos que a força de atrito f 21 (força de atrito que 2 faz em 1 ) forma um par com a força f 12 (força de atrito que 1 faz em 2 ), além desse par temos referente a normal do bloco 1 ( n 1 ) causada pelo contato com 2 , logo teremos uma reação igual e de sentido contrário em 2 , como mostra o diagrama.

Agora para achar o tempo mínimo pedido no enunciado basta usarmos a seguinte equação da cinemática:

x 1 = x 0 + v 0 x t 1 - t 0 + 1 2 a t 1 - t 0 2

Onde t 1 é o que queremos saber, já temos os valores de bem dizer quase tudo, só falta a aceleração a do bloco 2 .

Queremos a aceleração de 2 já que se ele completar o percurso de 5   m o bloco 1 estará junto, pois ele está sendo puxado e eles vão ter a mesma aceleração se 1 não escorregar em 2 . E também porque não sabemos o valor F para encontrarmos a aceleração através de 1 .

Com esses detalhes podemos usar a segunda lei de Newton para encontrar a aceleração sofrida pelo bloco 2 .

Passo 2

Primeiro vamos analisar o bloco 1 na direção y , para encontrarmos uma expressão para n 1 , já que ela aprece nos dois diagramas, temos o seguinte:

n 1 - m 1 g = 0

⇒ n 1 = m 1 g

Prontinho, era só isso mesmo kkkk.

Passo 3

Agora vamos analisar o bloco 2 na direção y , para encontrarmos uma expressão para n 2 , temos o seguinte:

n 2 - n 1 - m 2 g = 0

⇒ n 2 = n 1 + m 2 g

Substituindo n 1 pela expressão que encontramos no passo 1 temos:

n 2 = m 1 g + m 2 g

⇒ n 2 = m 1 + m 2 g

No próximo passo você vai entender o nosso interesse em achar expressões para as forças normais.

Passo 4

Agora vamos analisar ainda o bloco 2 só que na direção x , temos o seguinte:

m 2 a = f 12 - f 2

m 2 a = μ e 12 n 1 - μ c n 2

Onde μ e 12 é o coeficiente de atrito entre os blocos e μ c é o coeficiente de atrito entro o bloco 2 e o piso.

Agora você pode entender por que encontramos expressões para n 1 e n 2 . Substituindo essas expressões temos:

m 2 a = μ e 12 m 1 g - μ c m 1 + m 2 g

⇒ a = μ e 12 m 1 g - μ c m 1 + m 2 g m 2

Substituindo com os valores que sabemos, temos:

a = ( 0,6 ) ( 4 ) ( 9,8 ) - ( 0,2 ) 4 + 3 ( 9,8 ) 3

= 9,8 3

⇒ a = 3,267   m / s 2

Agora podemos encontrar o tempo que queríamos.

Passo 5

Agora vamos o último passo que é encontrar o tempo mínimo, temos:

x 1 = x 0 + v 0 x t 1 - t 0 + 1 2 a t 1 - t 0 2

Substituindo os valores conhecidos, temos:

5 = 0 + 0 t 1 - 0 + 1 2 3,267 t 1 - 0 2

⇒ 5 = 0 + 0 + 1,63 t 1 2

⇒ t 1 2 = 3,07

Então temos que:

t 1 = 1,75   s

Resposta

t 1 = 1,75   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

40. Uma caixa de 4,0k g , sobre uma rampa sem atrito e inclinada em 35°, está ligada a um peso de 20k g , suspenso, através de um barbante de massa desprezível que passa por uma polia, também sem mass
42. O bonde mostrado na FIGURA P7.42 desce uma colina de 200m de altura. Além dos freios, o bonde pode controlar sua velocidade puxando um contrapeso de 1.800k g que sobe simultaneamente pelo outro la
37. O bloco de 10,2k g da FIGURA P7.37 é mantido em repouso pela corda sem massa que passa por duas polias sem massa e livres de atrito. Determine os valores das tensões de T 1 a T 5 e o módulo da for
38. O coeficiente de atrito cinético entre o bloco de 2,0k g da FIGURA P7.38 e a mesa vale 0,30 . Quanto vale a aceleração do bloco de 2,0k g ?