Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 7.Exercícios e Problemas - Ex. 38
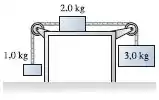
38. O coeficiente de atrito cinético entre o bloco de da FIGURA P7.38 e a mesa vale . Quanto vale a aceleração do bloco de ?
Passo 1
Então pessoal a base que precisamos para resolver esse problema é a segunda e a terceira lei de Newton, mas para sabermos como usá-las bem, vamos montar um diagrama de corpo livre para cada bloco do nosso sistema, temos o seguinte:
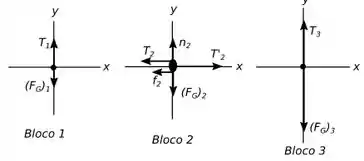
Vamos nos referir ao bloco da esquerda como bloco , o do meio como bloco e o da direita como bloco .
Agora vamos analisar a nossa situação junto com o diagrama para ver se temos forças iguais presentes.
Como as duas cordas e as polias não têm massa e não são deformadas temos que e que .
Uma coisa interessante a se notar é que como as cordas são ideias, todos tem o mesmo módulo de aceleração ,mas no caso do bloco teremos já que esse bloco acelera na direção negativa de .
Agora para achar a aceleração vamos analisar as forças de cada bloco usando a segunda lei de Newton e depois juntar as informações que obtemos.
Passo 2
Vamos começar analisando o bloco , como ele só se move na direção e não tem nenhuma interação na direção , vamos analisar apenas em , temos:
Bem simples por sinal kkkk.
Passo 3
Agora vamos analisar o bloco . Vamos começar com a direção , temos:
Então temos que:
Agora vamos analisar na direção , temos o seguinte:
Lembrando que essa força de atrito é cinética, vamos substituída pela sua expressão, temos:
Agora usando a expressão que achamos para , ficamos com:
Passo 4
Vamos analisar o bloco , como ele só se move na direção e não tem nenhuma interação na direção , vamos analisar apenas em , temos:
Esse também foi bem simples kkkk.
Passo 5
Então de equações que podemos considerar importantes que encontramos são essas três:
Agora vamos usar o fato de que , elas ficam assim:
Agora lembrando que e que , vamos somar as duas primeiras equações, assim:
Agora vamos pegar essa equação e subtrair a terceira equação que temos mais acima dela, assim ficamos com:
Agora vamos isolar e depois substituir os valores que conhecemos, temos: