Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 16.1 - Ex. 78
Dois pulsos de onda progressivos em uma corda são representados pelas funções de onda
e
Onde está em metros e está em segundos. (a) Usando uma planilha eletrônica ou uma calculadora gráfica, faça gráficos separados de cada uma das funções de onda como função de , em e em , e descreva o comportamento de cada uma com o aumento do tempo. (b) Faça um gráfico da função de onda resultante em , em e em .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Um esboço dos dados inseridos na planilha está exposto abaixo:
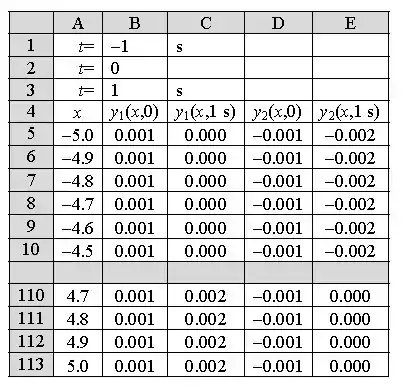
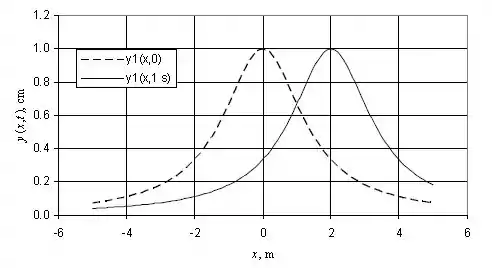
O gráfico de , deve ficar desta maneira:
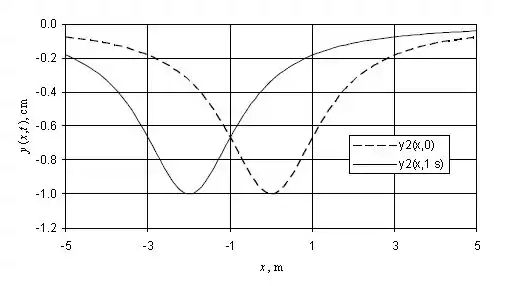
O gráfico de , deve ficar desta maneira:
Passo 2
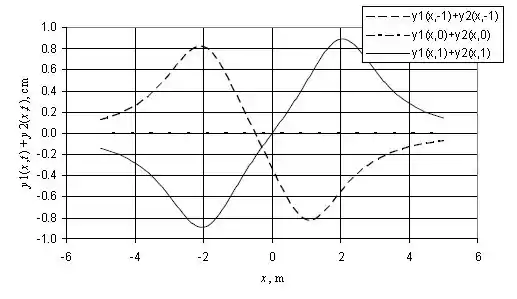
Item (b):
Abaixo está exposto o gráfico com a função da onda resultante para , e .
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
A Figura mostra a aceleração transversal do ponto x=0 de uma corda com função do tempo t , quando uma onda com a forma geral y x , t = y m s e n ( k x - ω t + ϕ ) passa pelo ponto. A escala do eixo ve
Uma onda senoidal transversal que se propaga no sentido negativo de um eixo x tem uma amplitude de 1,00c m , uma freqüência de 550H z e uma velocidade de 330m / s . Se a equação da onda é da forma y x
Uma onda humana. A ola é uma onda, criada pela torcida, que se propaga nos estádios em eventos esportivos (Figura). Quando a onda chega a um grupo de espectadores, eles ficam em pé com os braços levan
Uma onda possui uma frequência angular de 110r a d / s e um comprimento de onda de 1,80m . Calcule (a) o número de onda e (b) a velocidade da onda.
Um escorpião da areia pode detectar a presença de um besouro (sua presa) pelas ondas que o movimento do besouro produz na superfície da areia (Figura). As ondas são de dois tipos: transversais, que se