Exercícios de Equação Diferencial da Onda - Lista de Exercícios Resolvida
Questão 1
Use a equação de onda para determinar a velocidade de uma onda dada por:
Ver solução completaQuestão 2
Em uma corda ideal é produzida a seguinte perturbação:
Onde o eixo é horizontal e aponta para a direita e e são constantes positivas. Podemos afirmar que esta perturbação
- Não representa uma onda em propagação
- É a superposição de duas ondas que se propagam em sentidos opostos
- É uma onda que se propaga para a direita com velocidade
- É uma onda que se propaga para a esquerda com velocidade
- É uma onda que se propaga para a direita com velocidade
- É uma onda que se propaga para a esquerda com velocidade
- É uma onda que se propaga par a direita com velocidade
- É uma onda que se propaga para a esquerda com velocidade
Questão 3
Considere uma corda cuja tensão e a densidade linear são dadas por e , respectivamente, e a equação de movimento é representada por
- Considerando uma onda nesta corda escrita por
- Qual é o período da onda? Tem que justificar a definição do período utilizado.
Obtenha em termos de e .
Questão 4
Qual das seguintes funções é uma solução para a equação de onda, sendo e constantes reais?
Questão 5
Use a equação de onda para determinar a velocidade de uma onda dada por
Ver solução completaQuestão 6
Marque a opção que NÃO representa uma solução da equação de onda para uma corda. Considere que as constantes e são todas diferentes de zero:
Questão 7
Qual das seguintes funções é uma solução para a equação de onda, sendo e constantes reais?
Questão 8
A função de uma onda harmônica numa corda é:
Em que sentido a onda avança e qual a aceleração máxima de um ponto da corda?
(A) sentido negativo do eixo sendo
(B) sentido positivo do eixo sendo
(C) sentido negativo do eixo sendo
(D) sentido positivo do eixo sendo
(E) sentido negativo do eixo sendo
Ver solução completaQuestão 9
Três ondas propagantes senoidais estão em cordas idênticas, com a mesma tensão. As formas matemáticas das ondas são:
onde está em metros e em segundos. Faça a correspondência de cada forma matemática ao gráfico apropriado abaixo.
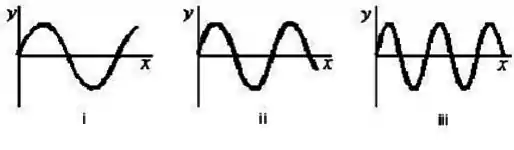
Questão 10
Dadas as seguintes funções:
Quais representam uma onda?
- Apenas
- Apenas
Questão 11
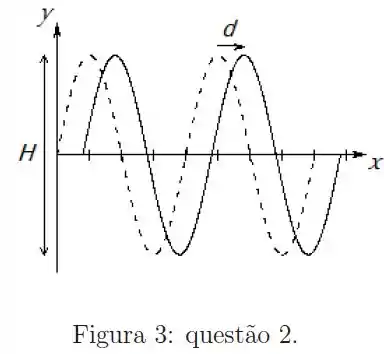
a) Mostre, por substituição direta, que (onde , são constantes) é solução da equação de onda se e determine a velocidade da onda em termos do comprimento de onda e do período .
A figura 3 mostra o deslocamento tranversal ao longo de uma corda que suporta uma onda harmônica como a descrita no item anterior, em dois instantes de tempo, . Durante este intervalo de tempo, as cristas da onda deslocam-se de uma distância , como indica a figura. Nela, cada divisão do eixo horizontal vale e a distância entre as cristas e os vales é de .
b)Determine a amplitude da onda .
c)Determine o número de onda .
d)Determine a frequência angular .
e)Determine a constante de fase da onda.
Questão 12
Um pulso numa corda é descrito pela função:
Onde são dados em cm e t em segundos.
a) Calcule a velocidade do pulso e determine em que sentido ele se propaga.
b) Determine a velocidade dos pontos da corda em função de x e t e calcule essa velocidade em x = 0 e t = 0.
c) Encontre uma função de onda que descreva o pulso de mesma forma mas que se propaga em sentido oposto.
Ver solução completaQuestão 13
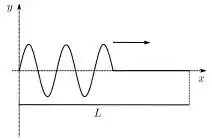
Uma corda de comprimento tem o extremo em fixo e o extremo emlivre. Quando vibra em um de seus modos normais, um ponto da corda num ventre oscila dez vezes por segundo e seu deslocamento atinge o valor máximo de . A distância entre ventres adjacentes vale .
a) Determine o comprimento de onda bem como a velocidade de propagação das ondas nesta corda.
b) Faça um esboço do perfil da corda neste modo de vibração, no instante em que todos os seus pontos têm deslocamento máximo. Indique claramente a posição de cada nó.
c) Escreva as expressões para a velocidade transversal dos pontos extremos da corda. Considere para a constante de fase da parte temporal de .
Ver solução completaQuestão 14
Uma corda de comprimento tem massa e está submetida a uma tração , com o extremo em preso a um suporte numa parede. Uma onda é produzida nesta corda ao movimentar-se seu extremo em num movimento harmônico com um período de . No instante esta extremidade da corda passava por com velocidade .
a) Calcule a velocidade de propagação , a frequência angular e o comprimento de onda da onda formada na corda.
b) Escrevendo a função de onda na forma , determine a amplitude e a constante de fase desta onda, antes que ela atinja o outro extremo em .
Onde aplicável, a resposta pode ficar em função de .
Ver solução completaQuestão 15
Quatro ondas progressivas são descritas pelas seguintes equações, onde todas as grandezas são medidas em
unidades SI. Quais dessas ondas têm o mesmo período?
- I e III, e também II e IV
- I e IV, e também II e III
- I e II, e também III e IV
- Todas elas têm o mesmo período.
- Todos elas têm períodos diferentes
Questão 16
Uma perturbação pode ser escrita na forma
Essa expressão:
a) não representa uma onda em propagação.
b) representa uma onda que se propaga com v = a.
c) representa uma onda que se propaga com v = a/b.
d) representa uma onda que se propaga com v = b.
e) representa uma onda que se propaga com v = 1/b.
Ver solução completaQuestão 17
Considere as seguintes funções y(x; t):
I. y(x; t) = 2
II. y(x; t) = cos (x) sin (t)+cos (4x) sin (4t)
III. y(x; t) = sin (5x - t) + 4 cos (5x - t)
IV. y(x; t) = 3 cos (2x) sin (10t)
Assinale a alternativa correta:
(a) I representa uma onda progressiva viajando da esquerda para direita.
(b) II não representa uma onda.
(c) III representa uma superposição de duas ondas estacionárias.
(d) IV representa uma onda estacionária.
Ver solução completa