A Figura mostra a aceleração transversal do ponto x=0 de uma corda com função do tempo t , quando uma onda com a forma geral y x , t = y m s e n ( k x - ω t + ϕ ) passa pelo ponto. A escala do eixo vertical é definida por a s = 400m / s ² ². Qual é o valor de ϕ ?

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 16.Problemas Adicionais - Ex. 70

A Figura mostra a aceleração transversal do ponto de uma corda com função do tempo , quando uma onda com a forma geral passa pelo ponto. A escala do eixo vertical é definida por . Qual é o valor de ?

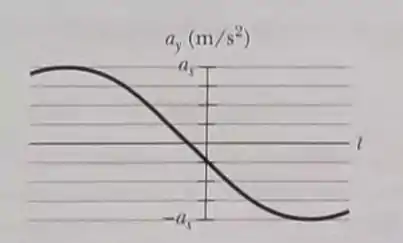
Passo 1

Bora lembrar de algumas coisas importantes. A primeira delas é que a aceleração de um corpo executando um movimento harmônico, distanciado de seu ponto de equilíbrio a uma distância igual a é dada por:

Analisando o ponto em que (caso dessa questão), a gente tem:

Passo 2

Além disso, em , a gente observa que a derivada da aceleração com relação ao tempo é negativa (pois a inclinação do gráfico está pra baixo nesse instante):

Então

Olha uma coisa importante que encontramos:. Isso nos mostra implicitamente que está no segundo ou no terceiro quadrantes.

Passo 3

Ok! Vamos continuar nossa análise. O gráfico mostra que em . Além disso, a aceleração máxima é a maior alcançada pelo gráfico e é igual a . Então, a gente consegue escrever a aceleração no ponto da seguinte forma:

Em :

Então:

Qual a resposta correta?

É aquela que corresponde a um dos quadrantes que comentamos no passo 1. Isso acontece com , que está no segundo quadrante.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois pulsos de onda progressivos em uma corda são representados pelas funções de onda y 1 x , t = 0,020 2,0 + ( x - 2,0 t ) ² ² e y 2 x , t = - 0,020 2,0 + ( x + 2,0 t ) ² ²Onde x está em metros e t e

Uma onda de pressão harmônica, produzida por uma fonte distante, tem, na região onde você se encontra, frentes de onda planas e vertiais. Faça o sentido + x apontar para o leste e o sentido + y aponta

Escreva um programa de planilha eletrônica para calcular e plotar a função y x = 4 π s e n x - s e n 3 x 9 + s e n 5 x 25 - … = 4 π ∑ n - 1 n s e n 2 n + 1 x 2 n + 1 2 Para 0 ≤ x ≤ 4 π . Use apenas os

Em princípio, uma onda com praticamente qualquer forma arbitrária pode ser expressa como uma soma de ondas harmônicas de diferentes frequências. (a) Considere a função definida por f x = 4 π c o s x 1

Um fio de 2,00m de comprimento, fixo nas duas extremidades está vibrando em seu modo fundamental. A tração no fiio é de 40,0N e a massa do fio é de 0,100k g . A amplitude no meio do fio é de 2,00c m .