Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 16.1 - Ex. 4

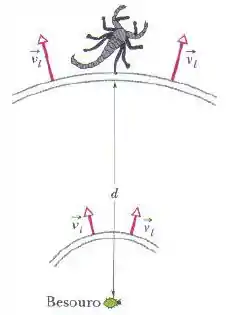
Um escorpião da areia pode detectar a presença de um besouro (sua presa) pelas ondas que o movimento do besouro produz na superfície da areia (Figura). As ondas são de dois tipos: transversais, que se propagam com uma velocidade v t = 50   m / s , e ondas longitudinais, que se propagam com uma velocidade v l = 150   m / s . Se um movimento brusco produz essas ondas, o escorpião é capaz de determinar a que distância se encontra o besouro a partir da diferença ∆ t entre os instantes em que as duas ondas chegam à perna que está mais próxima do besouro. Se ∆ t = 4,0   m s , a que distância está o besouro?

Passo 1

Fala galerinha do RespondeAí, tudo beleza?

Primeiro vamos lembrar como a velocidade e a distância se relacionam. Voltando lá na Física I, a gente descobre que:

d = v t

Onde d é a distância percorrida, v é a velocidade e t é o tempo.

No nosso caso, temos duas ondas com velocidades diferentes:

v 1 = 50   m/s

v 2 = 150   m/s

E o escorpião só consegue detectar a diferença de tempo entre elas, ou seja, só consegue detectar esse valor aqui:

Δ t = t 1 - t 2

Passo 2

Beleza, se a gente juntar tudo que a questão deu de informação e usar as fórmula que falamos ali em cima, vamos chegar em um sistema:

d = 50 t 1

d = 150 t 2

Logo:

Δ t = t 1 - t 2

Δ t = 4 × 10 - 3   s

Então temos um sistema com três equações e três incógnitas: Bora lá ver resolver essa brincadeira

Passo 3

Iradoso, se a gente igualar as duas primeiras equações (já que as duas são iguais à d ):

50 t 1 = 150 t 2

t 1 = 150 50 t 2

t 1 = 3 t 2

E substituir isso na segunda equação:

t 1 - t 2 = 4 × 10 - 3   s

3 t 2 - t 2 = 4 × 10 - 3   s

2 t 2 = 4 × 10 - 3   s

Logo:

t 2 = 2 × 10 - 3   s

E agora é só substituir lá em cima de novo pra achar o valor de d .

d = 150 t 2

d = 150 2 × 10 - 3 = 300 × 10 - 3   m

d = 3,0 × 10 - 1   m

Ou em centímetros:

d = 30   cm

Resposta

d = 30   cm

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que a função y = A s e n k x cos ⁡ ω t satisfaz à equação de onda.
Mostre, explicitamente, que as seguintes funções satisfazem à equação da onda ∂ 2 y ∂ x 2 = 1 v 2 ⋅ ∂ 2 y ∂ t 2 :(a) y x , t= k x + v t 3 (b) y x ,t = A e i k x - v t (c) y x ,t = ln ⁡ k x - v t
Dois pulsos de ondas retangulares viajam em sentidos opostos ao longo de uma corda. Em t = 0 , os dois pulsos estão como mostrado na figura. Esboce as funções de onda para t = 1,0 ; 2,0 e 3,0 s .
Repita o problema 1 para o caso em que o pulso da direita é invertido.
Um diapasão, com frequência natural f 0 , começa a vibrar no tempo t = 0 e é parado após um intervalo de tempo ∆ t . A forma de onda do som, em algum tempo posterior, é mostrada (Figura 16-35) como fu