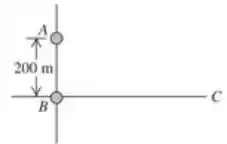
Duas antenas de rádio irradiam em fase e estão localizadas nos pontos e separados por uma distância de (Figura 35.23). As ondas de rádio têm uma frequência igual a . Um receptor de rádio é deslocado de , sendo movido ao longo de uma reta perpendicular ao segmento que liga os pontos e (reta da Figura 35.23). A que distâcia de ocorrerá interferência destrutiva? (Nota: a distância entre o receptor e a fonte não é grande em comparação com a distância entre as fontes, de modo que a Equação (35.5) não pode ser aplicada.)
Passo 1
Bom, a gente sabe que a interferência destrutiva acontece quando a diferença de caminho das duas ondas que chegam até o receptor segue essa fórmula aqui:
Então vamos fazer um desenho pra ajudar a calcular essa diferença de caminho:
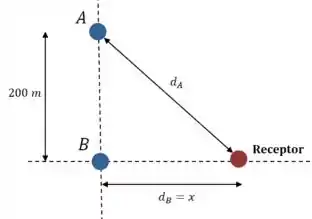
Passo 2
Ok, agora vamos fazer um pouco de álgebra. Igualando as duas expressões do passo de cima, ficamos com o seguinte:
Isolando a raiz quadrada:
E elevando os dois lados ao quadrado:
E agora isolando :
Você pode calcular o comprimento de onda a partir da frequência:
Obs.: O enunciado menciona uma frequência de , mas nesse caso o comprimento de onda estaria na casa dos milhares de quilômetros (não faz sentido nesse problema!).
E por isso usamos , que dá um comprimento mais razoável para esse problema, e que faz sentido para ondas de rádio.
Passo 3
Então vamos ver os valores de que aparecem para .
O que a gente quer calcular é a primeira posição de em que a intereferência acontece, então vamos começar com os valores mais altos de .
Quando :
Esse resultado já não faz sentido, porque pela nossa definição só pode ser positivo.
Então vamos tentar com :
Beleza, então essa é a primeira posição de interferência destrutiva.
Resposta
A interferência acontece quando o receptor está a de .