Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 35.Problemas - Ex. 39
O raio de curvatura da superfície convexa de uma lente plano-convexa é igual a . A lente é colocada com a face conexa apoiada sobre uma placa de vidro perfeitamente pana e iluminada verticalmente de cima para baixo com luz vermelha de comprimento de onda igual a . Calcule o diâmetro do segundo anel brilhante da figura de interferência.
Passo 1
Vamos começar tentando entender de onde vem a interferência nesse problema. Esse desenho está bem exagerado, mas ajuda a ilustrar:
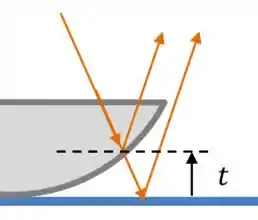
Vamos ter uma diferença de caminho entre os raios que são refletidos pela parte azul (a placa de vidro plana) ou pela lente convexa.
Já que a reflexão entre esses meios vai causar uma diferença de fase, a interferência construtiva vai acontecer quando:
E usando um pouco de geometria, dá pra achar uma expressão pra esse :
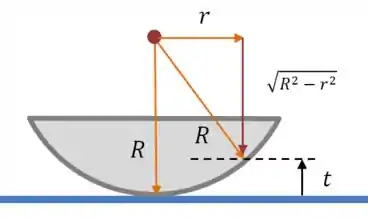
Então:
Passo 2
Beleza, agora vamos usar essas duas equações. Primeiro isolamos na primeira:
E juntando isso com a segunda equação:
Vamos isolar a raiz pra poder elevar tudo ao quadrado e fazer ela sumir:
Elevando os dois lados ao quadrado:
Agora já podemos isolar o raio :
Quando , dá pra desprezar o termo da direita:
Então:
Passo 3
Beleza, agora finalmente podemos calcular o raio do anel. O segundo anel mais brilhante é , já que o primeiro é :
Substituindo os outros valores numéricos convertidos para metros:
Esse é o raio do anel, então o diâmetro é:
Resposta
O diâmetro do segundo anel brilhante é .