Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 21.Problemas Adicionais - Ex. 61
Duas cargas pontuais de e são mantidas fixas no eixo , na origem e no ponto , respectivamente. Uma partícula com uma carga de é liberada a partir do repouso no ponto . Se a aceleração inicial da partícula é , qual é a massa da partícula?
Passo 1
E aí, galerinha! 😊
O enunciado nos fala de duas partículas que estão fixadas em duas posições, e aí tem outra partícula que parte do repouso de uma posição com uma aceleração inicial e ele quer saber a massa da partícula, certo? Então fica assim o desenho:
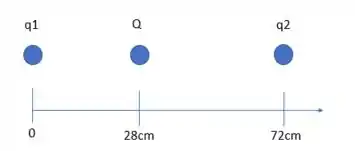
Nós devemos calcular o módulo das forças exercidas pelas duas cargas fixadas na carga que entrará em movimento. Chamaremos as partículas que estão fixadas de e , ok? E chamaremos a carga em movimento de Q. Para calcular força devido a cargas nós utilizaremos a famosa Lei de Coulomb:
Onde: é a força aplicada no corpo; é a constante de Coulomb e vale; é a carga da primeira partícula; é a carga da segunda partícula e é a distância entre as duas partículas.
Portanto, nós devemos calcular o módulo da força total sobre a carga que entrará em movimento, e depois usar a famosíssima 1° Lei de Newton
para achar a massa, já que o enunciado já dá a aceleração.
Veja só! 😉
Passo 2
Iremos calcular o módulo da força eletrostática total que é exercida na carga .
Uma coisa muito importante que devemos lembrar é que cargas de mesmo sinal se repelem, enquanto cargas de sinais diferentes se atraem, então vamos olhar nossas cargas:
(positiva)
(negativa)
(positiva)
Pensando só na força entre as cargas e , como as duas partículas são positivas, elas se repelem. Logo a força que a carga gera na carga tem o seguinte sentido:
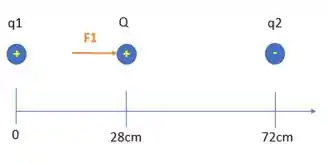
E quanto vale essa força? Vamos aplicar nossos valores na fórmula que já falamos para encontrar a força:
Concorda comigo que a distância entre as duas cargas será:
Substituindo essa informação na fórmula:
Encontramos a primeira força, parabéns! Vamos encontrar a segunda? Vamos lá!
Passo 3
Agora pensando só na força entre as cargas e , como as duas partículas são de sinais diferentes, elas se atraem. Logo a força que a carga gera na carga tem o seguinte sentido:
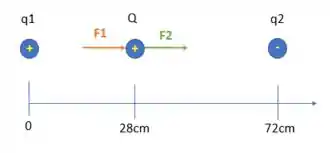
E quanto vale essa força? Vamos aplicar nossos valores na fórmula que já falamos para encontrar a força:
Concorda comigo que a distância entre as duas cargas será:
Substituindo essa informação na fórmula:
Repare que a força exercida pela carga 1 e 2 tem mesmo sentido, por isso basta que a gente some o módulo das forças 😊, dessa forma:
Bacana, não é? 😉
Passo 4
Da 1° Lei de Newton, temos:
Força é igual a multiplicação entre a massa e a aceleração . Logo, podemos encontrar a massa se já sabemos a força total aplicada na partícula que desejamos e sua aceleração:
Substituindo o valor de força encontrado no passo 2 e o valor de aceleração ao ser solta do repouso dana no enunciado (), temos:
Vamos transformar de km para metros:
E aí! o que achou? Responde Aí! 😁
