Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 21.4 - Ex. 11
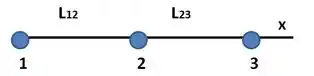
Na Fig. 21-24, três partículas carregadas estão em um eixo . As partículas e são mantidas fixas. A partícula está livre para se mover, mas a força eletrostática exercida sobre ela pelas partículas e é zero. Se , qual é o valor da razão ?
Passo 1
Fala aí! como vai? 😁
Nesse problema temos três partículas carregadas no eixo sendo que as partículas e são mantidas fixas e a partícula está livre para se mover, mas a força eletrostática exercida sobre ela pelas partículas e é zero.
Dessa forma Se , queremos saber qual é o valor da razão .
Tem ideia de como fazemos isso? 🤔
Você deve estar se perguntando: e, agora, como resolver se os valores das cargas nem os sinais delas foram fornecidos? Tá brincando comigo?
Calma! Vamos resolver a questão naturalmente, usando a soma vetorial das forças que as cargas e exercem sobre a . Para isso, vamos batizar essas forças de e . Como a soma dessas forças é nula (o que foi dito no enunciado), a gente tem que:
Sendo e as formas vetoriais dessas forças, tais que:
E
Já que elas só exercem força em .
Veja só! 😉
Passo 2
Beleza! Vamos agora usar a expressão:
E substituir os valores que encontramos no passo anterior:
Repare que podemos dividir a equação acima por . Fazendo isso, sobra o seguinte:
Como , vem:
Tranquilo até aqui? 😎
Passo 3
Quase lá!
Multiplicando a expressão do passo anterior por , sobra:
Ou seja, para que o lado esquerdo da equação seja , deve ser , já que o vetor unitário nunca será nulo:
Dividindo agora essa equação por , a gente fica com o seguinte:
Com isso:
Isso significa que as cargas e devem ter sinais opostos e que o módulo de é quatro vezes maior que o de E isso não depende do valor de !
Show! Vamos pra próxima!
