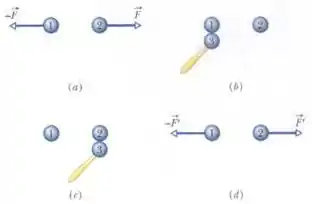
Duas esferas condutoras de mesmo diâmetro, e , possuem cargas iguais e estão separadas por uma distância muito maior que o diâmetro (Figura. 21-22a). A força eletrostática a que a esfera está submetida devido à presença da esfera é . Uma terceira esfera , igual às duas primeiras, que dispõe de um cabo não condutor e está inicialmente neutra, é colocada em contato primeiro com a esfera (Figura 21-22b), depois com a esfera (Fig. 21-22c) e, finalmente, removida (Figura 21-22d). A força eletrostática que a esfera agora está submetida tem módulo . Qual é o valor da razão ?

E aí, pessoal! 😁

Nesse problema temos duas eseras condutoras idênticas de mesma carga e a força eletrostática entre elas é . Uma terceira esfera idêntica e neutra entra em contato com a primeira carga até estarem em equilíbrio e depois essa terceira esfera entra em contato com a segunda esfera. Depois desses contatos, a força eletrostática entre as esferas e é e nosso objetivo é obter .

Tem ideia de como fazemos isso? 👀

Vamos interpretar cada etapa do problema...

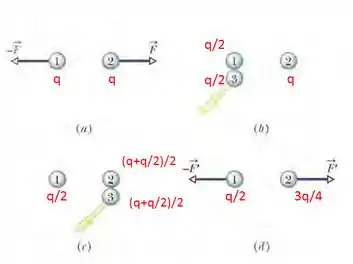
Repare, primeiro, nas etapas (a) e (b): Depois que as esferas e encostam-se, como elas são iguais, a carga é distribuída igualmente entre elas. Por isso, cada uma fica com depois do contato. A mesma coisa acontece em (c), com as esferas e A soma das cargas que elas possuíam antes do contato é distribuída igualmente entre elas. Por isso, cada uma leva depois da interação.

Legal, né? 😊