Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 28.Exercício - Ex. 6
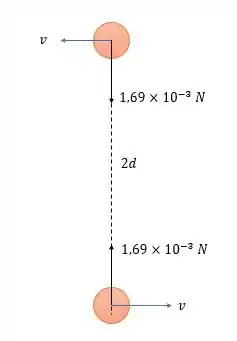
6- Duas cargas puntiformes positivas, e , se movem em relação a um observador situado no ponto , como indica a Figura . A distância é igual a e .
Quando as cargas estão nos pontos indicados na figura, qual é o módulo, a direção e o sentido do campo magnético resultante que elas produzem no ponto ?
Quais são o módulo, a direção e o sentido das forças elétricas e magnéticas que cada carga exerce sobre a outra, e qual é a razão entre o módulo da força elétrica e o módulo da força magnética?
Se o sentido de for invertido, de modo que ambas as cargas se desloquem no mesmo sentido, quais são o módulo, a direção e o sentido das forças magnéticas que as duas cargas exercem entre si?
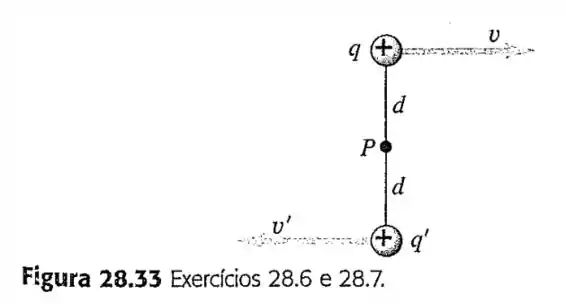
Passo 1
Considerando o ponto a origem do plano cartesiano nós teremos a seguinte representação vetorial do problema.
Então:
Pois a distância é sempre partindo da carga até o ponto de interesse, entre para a partícula de carga sabemos que será negativa em .
Cortando os temos:
Então sabemos de certeza que o sentido desse campo é entrando na folha pois todos os valores serão positivos. Então substituindo tudo nós teremos:
O módulo será de .
Passo 2
A força elétrica é mais simples e para calcular basta fazer:
Onde e então:
E como as duas cargas são positivas então elas sofrem repulsão de modo que na carga de temos um sentido para cima e na temos sentido para baixo, da seguinte forma.
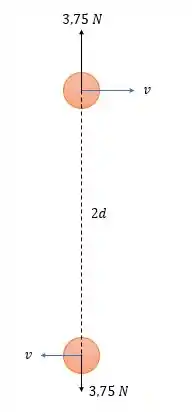
Passo 3
Já a força magnética seria calculada como:
Isso para uma partícula.
Porém será causada pelo movimento da outra partícula então teremos uma coisa do tipo:
Logo o módulo disso será:
Como encontramos que entra na folha então pela regra da mão esquerda a força magnética na carga aponta para cima e na aponta para baixo da seguinte forma (caracterizando em uma força repulsiva):
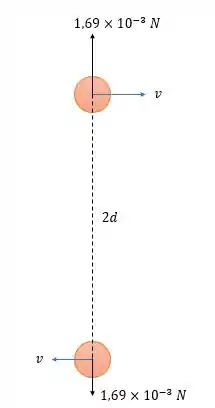
A razão entre as duas forças se dará por:
Passo 4
Invertendo a velocidade nas duas cargas (pela regra da mão esquerda) nós teremos uma força magnética de atração e de mesma intensidade igual a da seguinte forma:
