Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.2 - Ex. 28b

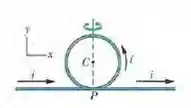
Na figura 29-56, parte de um fio longo isolado que conduz uma corrente i = 5,78   m A é encurvada para formar uma espira circular de raio R = 1,89   c m . Em termos dos vetores unitários, determine o campo magnético C no centro da espira (b) se a espira está perpendicular ao plano do papel.

Passo 1

Fala aí! como vai? 😉

Nesse problema temos um fio longo onde é feito um loop em um ponto formando uma espira de raio R = 1,89 c m . O fio é percorrido por uma corrente de i = 5,78 m A e a espira está perpendicular ao plano do papel.

A partir daí queremos saber qual é o campo magnético no centro da espira.

Parece complicado, não é? 👀

Para simplificar o problema, podemos considerar dois fios distintos e consequentemente duas contribuições distintas... uma para a espira e outra para o fio retilíneo longo.

Para a espira, a contribuição pode ser obtida a partir da lei de Ampere como

B C 1 = μ o i 2 R

Já para o fio retilíneo, a contribuição pode ser calculada como

B C 2 = μ o i 2 π R

Veja só! 😁

Passo 2

Nesse caso, B C 1 → é perpendicular a B C 2 → e, portanto,

B C = B C 1 2 + B C 2 2

B C = μ o i 2 R 2 + μ o i 2 π R 2

B C = μ o i 2 R 2 1 + 1 π 2

Simplificando...

B C = μ o i 2 R 1 + 1 π 2

Substituindo os valores do enunciado, temos

B C = 4 π × 10 - 7 T . m A 5,78 × 10 - 3   A 2 0,0189   m 1 + 1 π 2 B C = 2,02 × 10 - 7   T

Tranquilo até aqui? 😉

Passo 3

E B C → faz uma ângulo com o plano do papel dado por:

θ = tan - 1 ⁡ B C 1 B C 2 = t a n - 1 1 π = 17,66 °

Na notação dos vetores unitários,

B C → = 2,02 × 10 - 7   T cos ⁡ 17,66 ° i ^ + s e n 17,66 ° k ^

B C → = 1,92 × 10 - 7 T i ^ + 6,12 × 10 - 8   T k ^ B C → = 192   n T i ^ + ( 61,2   n T ) k ^  

E aí! entendeu tudo? Responde Aí! 😬

Resposta

O campo magnétigo no centro da espira é:

B C → = 192   n T i ^ + ( 61,2   n T ) k ^  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

7- A figura 28.33 mostra duas cargas puntiformes, q e q ' , que se movem em relação a um observador situado no ponto P . Suponha que a carga inferior seja negativa, com q ' = - q . ( a ) Calcule o mód
8- Um elétron e um protón se movem a 845k m / s cada um, em trajetórias perpendiculares, como indica a Figura 28.34 . No instante em que eles estão nas posições indicadas na figura, determine o módulo
18- Dois fios retilíneos longos, um situado acima do outro, estão em uma direção paralela ao eixo O x ; e a distância entre eles é igual a 2 a . Considere um eixo + O y situado no plano dos fios e ori
6- Duas cargas puntiformes positivas, q = + 8.0μ C e q ' = + 3.0μ C , se movem em relação a um observador situado no ponto P , como indica a Figura 28.33 . A distância d é igual a 0.120m ,v = 4.50 × 1
10- Um fio retilíneo longo, que transporta uma corrente de 200A , atravessa uma caixa cúbica de madeira, entrando e saindo através de furos situados nos centros de duas faces opostas (Figura 28.36 ).