Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 28.Exercício - Ex. 10
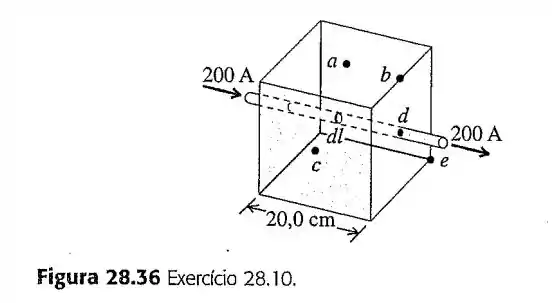
10- Um fio retilíneo longo, que transporta uma corrente de , atravessa uma caixa cúbica de madeira, entrando e saindo através de furos situados nos centros de duas faces opostas (Figura ). A aresta da caixa é igual a . Considere um comprimento do fio igual a no centro da caixa.
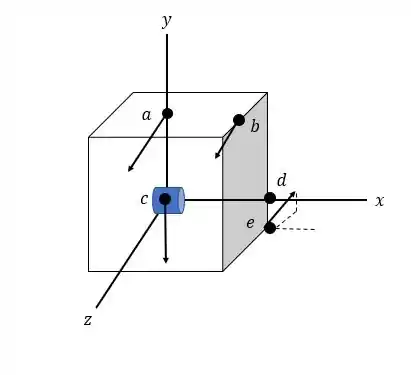
Calcule o módulo do campo magnético produzido por esse elementos nos pontos , indicados na Figura . Os pontos e estão nos centros das faces do cubo; a ponto está no meio de uma das arestas; e o ponto está sobre um vértice. Copie a figura e mostre as direções e os módulos relativos de cada vetor do campo magnético. (Nota: suponha que seja pequeno em comparação as distâncias entre o elemento de corrente o ponto onde o campo magnético é calculado.)
Passo 1
Vamos primeiro anotar os dados por que a questão é grande:
está no meio da caixa (podemos considerar como a origem)
Fórmulaa ser aplicada:
Por mais que sejam simples os pontos vamos fazer da forma vetorial para que fique mais fácil de visualizar os sentidos e direções do campo magnético.
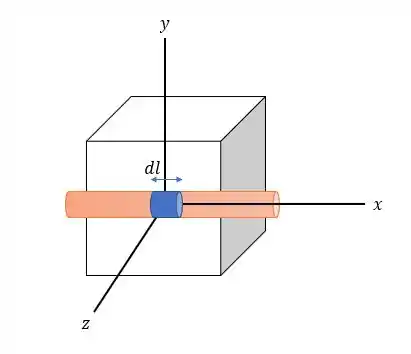
Considerando a origem do sistema cartesiano em e o sistema de coordenadas desenhado na figura acima teremos os seguintes valores de e de para cada ponto no cubo.
Passo 2
Calculando agora o campo magnético em cada ponto nós temos:
Isso quer dizer que o campo magnético em apontará para a direção de , mas vamos fazer os desenhos depois primeiro vamos fazer a mesma coisa para todos os campos. E segue a mesma direção da corrente, que no nosso sistema de coordenadas está aoponto para .
O campo magnético em também aponta para mas como está um pouco mais distante que o ponto então terá uma intensidade menor. Sem contar que multiplicação vetorial de com é nulo.
Agora para o campo em .
Esse ponto tem a mesma intensidade que em porém aponta negativamente para no nosso sistema de coordenadas.
Agora para :
Campo nulo, pois ele está na mesma direção da corrente, e multiplicação vetorial no mesmo eixo é nulo.
Agora finalmente para o ponto , o mais complexo nós temos:
Então esse vetor tem sentido em e de mesma intensidade, o módulo desse campo então será de:
Passo 3
Desenhando todos esses vetores no cubo nós teremos:
