Duas cargas puntiformes positivas, cada uma com módulo , são fixadas sobre o eixo nos pontos e . Considere zero o potencial a uma distância infinita das cargas. a)Faça um diagrama para montar as posições das cargas. b)Qual é o potencial na origem? c)Mostre que o potencial em qualquer ponto sobre o eixo x é dado por . d)Faça um gráfico do potencial sobre o eixo em função de de até . e)Qual é o potencial quando ? Explique como esse resultado é obtido.
Passo 1
letra a)
Como as cargas estão fixadas sobre o eixo nos pontos e , temos o seguinte desenho.
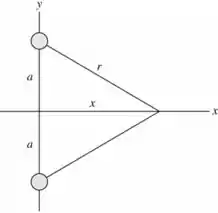
Passo 2
letra b)
O potencial elétrico é dado por:
Na origem o potencial será então:
Passo 3
letra c)
Vamos pegar agora o potencial em qualquer ponto do eixo
Se considerarmos o desenho do item (a), vemos que a distância será a hipotenusa do triângulo com os catetos e .
Então:
O potencial então será:
Passo 4
letra d)
Pela expressão do potencial, podemos perceber que o potencial aumenta conforme o módulo de diminui e o potencial terá um pico em . Então:
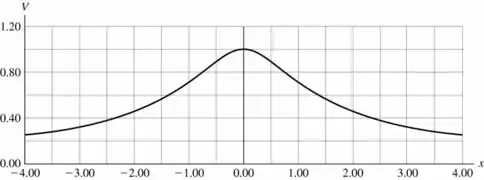
Passo 5
letra e)
Quando , podemos aproximar o potencial para:
Assim como uma carga pontual de carga. A uma distância das cargas muito maior que a separação, as duas cargas agem como uma carga pontual única.
Resposta
letra a)
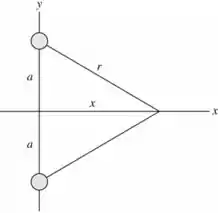
letra b)
letra d)
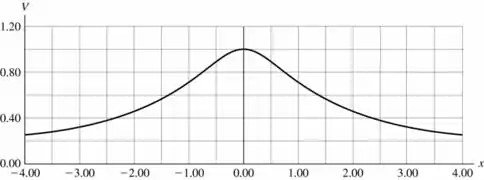
letra e)
Assim como uma carga pontual de carga. A uma distância das cargas muito maior que a separação, as duas cargas agem como uma carga pontual única.