Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 24.Problemas Adicionais - Ex. 102
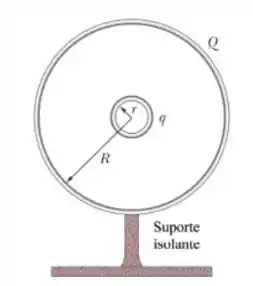
Na Fig. 24-71, uma casca esférica de metal com carga e raio está no centro de outra casca esférica de metal com carga e raio . (a) Qual a diferença de potencial entre as esferas? Se as esferas forem ligadas por um fio condutor, qual será a carga menor (b) na casca e (c) na casca maior?
Passo 1
Opa! Vamos pra mais uma questão!
Essa questão fala do potencial de duas cascas esféricas, então antes de qualquer coisa vamos lembrar qual é o potencial desse tipo de sistema, beleza? Usaremos a seguinte equação pra calcular o potencial:
Quando tivermos esferas concêntricas teremos que aplicar uma superposição de efeitos subtraindo o potencial de uma menos a outra.
Passo 2
E aí o potencial na superfície da esfera maior é
E da esfera menor é
A diferença de potencial é dada por
Substituindo os valores temos:
Por fim:
Passo 3
Agora vamos colocar essas duas esferas em contato por intermédio de um fio condutor.
O que vai acontecer aqui é que vai fluir carga de onde o potencial é maior até onde o potencial é menor até que as duas esferas tenham o mesmo potencial, ou seja, nesse caso aqui a carga da esfera maior vai diminuir e a da esfera menor vai aumentar até que as duas esferas tenham o mesmo potencial!
Vamos primeiro dar nome aos bois! Vamos chamar a carga final da esfera maior de e a carga final da esfera menor de .
Assim se as duas esferas têm o mesmo potencial, podemos dizer que
Substituindo os raios dessas esferas
Show! Achamos uma relação entre essas duas cargas!
Passo 4
Agora vamos achar outra relação por meio da conservação da carga! Como não tiramos nem adicionamos carga nesse sistema a soma total de cargas antes e depois de colocar esses fios tem que ser a mesma! Isso significa que
Como já temos e q
Agora é só jogar a relação do passo anterior!
E voltado para
Show! Terminamos mais! :D
Resposta
a)
b)
c)