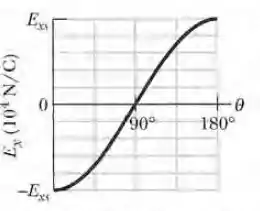
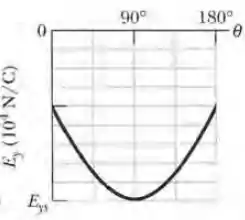
Duas contas carregadas estão sobre o anel da Fig. a que possui um raio R = 60,0 cm. A conta 2, que não aparece na figura, é mantida fixa. A conta 1 está inicialmente no eixo x, na posição , mas é deslocada para a extremidade oposta do anel, ou seja, para a posição , passando pelo primeiro e segundo quadrantes do sistema de coordenadas xy. A figura b mostra a componente x do campo elétrico produzido na origem pelas duas contas em função de e a Fig. c mostra a componente y do campo. As escalas dos eixos verticais são definidas por e (a) Qual é o ângulo da conta 2? Determine a carga (b) da conta 1 e (c) da conta 2.

(a)

(b)

©

Item (a)

Olhando para o gráfico da figura b, vemos que a componente x do campo total é nula para , isto é, quando a conta 1 está no semieixo y positivo. Isso só pode significar que a conta 2 está no semieixo y negativo, ou seja, que o ângulo da conta 2 é .

Item (b)

Bem, a componente y é máxima quando a conta 1 está com , como a carga da conta 2 é negativa, sabemos que a carga da conta 1 é positiva, pois as contas nessas posições, o módulo do campo elétrico é o maior no gráfico, o que indica que as componentes do campo elétrico se somaram.

Nos ângulos e , o valor absoluto da componente x é igual ao módulo do campo elétrico criado pela conta 1! Assim,

Como a carga da conta 1 é positiva e sabemos os valores do campo elétrico (, distância (, constante de Coulomb (, basta substituirmos e calcular:

Item (c)

Assim como fizemos no item b, quando a conta 1 está com ângulo , a componente y do campo elétrico devido a conta 1 é nula, portanto, o valor absoluto da componente y é igual ao módulo do campo elétrico criado pela conta 2. Assim, usando a mesma equação do passo 3, sabendo que a carga da conta 2 é negativa: