Duas cordas muito longas, bem esticadas, de densidades lineares diferentes e , estão ligadas uma à outra. Toma-se a posição de equilíbrio como eixo dos e a origem no ponto de junção, sendo o deslocamento transversal da corda. Uma onda harmônica progressiva, , viajando na corda (), incide sobre o ponto, de junção, fazendo-o oscilar com frequência angular . Isto produz na corda () uma onda progressiva de mesma frequência, (onda transmitida), e dá origem na corda 1, a uma onda que viaja em sentido contrário, (onda refletida). Dada a onda incidente , de amplitude , desejam-se obter a amplitude de reflexão , e a amplitude de transmissão . (a) Dada a tensão da corda, calcule as velocidades de propagação e nas cordas e , bem como os respectivos números de onda e . O deslocamento total na corda é , e na corda é . (b) Mostre que, no ponto de junção , deve-se ter . (c) Aplicando a lei de Newton ao ponto de junção , mostre que, nesse ponto, deve-se ter também . (d) A partir de (b) e (c), calcule as amplitudes de reflexão e transmissão e em função das velocidades e . Discuta o sinal de .

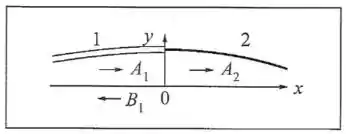
(b) No ponto de junção, podemos descrever o deslocamento transversal de duas formas.

Considerando as ondas que se propagam do lado esquerdo (incidente e refletida), temos:

E considerando a onda do lado direito (transmitida), temos:

Como há apenas um valor para o deslocamento transversal nesse ponto a cada instante, temos:

(c) Agora queremos usar a terceira lei de Newton (ação e reação) para encontrar uma condição de contorno para o ponto de junção.

Já que estamos falando da terceira lei de Newton no ponto de junção, vamos pensar na força que age sobre aquele ponto.

Vimos que ele tem deslocamento transversal dado por . A força que age sobre um ponto com deslocamento transversal em uma corda é:

Agora podemos escrever isso com qualquer uma das expressões que temos para :

Que é exatamente o que queríamos demonstrar.

(d) Vamos escrever equações para cada uma das ondas, de acordo com a notação que foi dada no enunciado.

Para a onda incidente, temos:

Para a onda refletida:

E para a onda transmitida:

E temos duas condições de contorno para aplicar:

Começamos aplicando a primeira:

E lembrando que :

Então:

E agora vamos aplicar a segunda. Primeiro precisamos derivar as expressões:

E essa relação é válida para , então:

E sabemos que , então:

E então ficamos com um sistema de duas equações para as amplitudes:

Vamos somas as duas equações:

E daqui podemos calcular a razão :

Multiplicando em cima e embaixo por :

Agora queremos calcular :

Vamos multiplicar a primeira equação por :

Então:

E a razão entre as amplitudes é:

Agora vamos substituir com as expressões para e :

Multiplicando em cima e embaixo por , ficamos com: