Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 2- Ed: 14º - Capítulo 15.Exercícios - Ex. 36

A distância entre dois ventres adjacentes de uma onda estacionária sobre uma corda é igual a 15,0 cm. Uma partícula situada em um ventre oscila em MHS com amplitude igual a 0,850 cm e período igual a 0,0750 s. A corda está sobre o eixo O x e se encontra fixa no ponto x = 0 . (a) Qual a distância entre os nós adjacentes? (b) Qual o comprimento de onda, a amplitude e a velocidade de duas ondas progressivas que adquirem esse padrão? (c) Calcule as velocidades transversais máxima e mínima de um ponto em um ventre. (d) Qual é a menor distância ao longo da corda entre um nó e um ventre?

Passo 1

Oii pessoal, show de bola??

“A loucura é como a gravidade, só precisa de um empurrãozinhooo...”

Bora empurrar e macetar essa questãozinha comigo agora

  1. A distância entre nós adjacentes é a mesma distância entre dois ventres adjacentes.

    2. Note que os nós são os pontos em que y   =   0 qualquer que seja o 1, isto é, os pontos que satisfazem s e n   ( k x ) = 0 . Os ventres são os pontos que oscilam com ampitude máxima.

    Como para um x fixo a amplitude do movimento dado por y   =   y ( t ) é   A E S   s e n   ( k x ) , os ventres, são, portanto, os pontos que satisfazem s e n   ( k x ) = 1 .

    Dessa forma, fica claro que a distância entre nós consecutivos é a mesma que de ventres consecutivos.

    Logo, a distância entre nós consecutivos é de d = 15   c m .

    Além disso, a distância entre nós adjacentes vai ser metade do comprimento da onda!

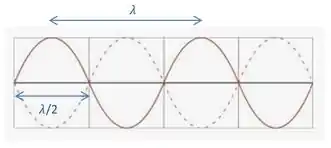
    Portanto,

    λ 2 = 15 c m

    λ = 30 c m

    Passo 2

  2. Neste problema iremos aplicar nossos conhecimentos sobre ondas estacionárias e modos normais. Iremos aplicar a equação da onda estacionária, e a relação entre a amplitude da onda estacionária com a onda original:

    3. y x , t = A E S   s e n   k s s e n   ( ω t )

    A E S = 2 A

    Vamos considerar as duas ondas progressivas de mesma amplitude e comprimento de onda e velocidades opostas, onde uma foi dada pela reflexão da outra gerando esse padrão de onda estacionária.

    Primeiramente vamos calcular a amplitude da onda progressiva original.

    O enunciado fornece dados quanto ao ventre.

    Como no ventre s e n   ( k x ) = 1 , podemos escrever o

    y = y t

    Por

    y t = A E S   s e n   ( ω t )

    Para ondas progressivas, a ideia é a mesma:

    λ 2 = 15

    ou seja,

    λ = 30 c m = 3,0 × 10 - 1 m .

    E como sabemos o período T = 0,075 s , podemos calcular a velocidade através da fórmula:

    v = λ f

    = λ T

    = 3,0 × 10 - 1 0,075

    = 4 m / s

    A amplitude vai ser a metade da onda fornecida:

    A = 1 2 0,85

    = 0,43 c m

    = 4,3 × 10 - 3 m

    Passo 3

  3. A velocidade transversal vai ser a derivada temporal da função de onda:

    4. ∂ y ∂ t = v y = A ω s e n k x   c o s ω t

    E vai ter valor máximo em v y = A ω e mínimo v y = 0 .

    Para determinar o valor máximo precisamos do valor de ω :

    ω = 2 π T

    = 2 π 0,075

    = 83,8 r a d / s

    Então

    v y , m á x = 0,85 × 10 - 2 ⋅ 83,8

    = 0,71 2 m / s

    v y , m í n = 0

    Passo 4

  4. Vamos aplicar nossos conhecimentos sobre nós e ventres em ondas estacionárias.

Já discutimos anteriormente que cada ventre se encontra bem no meio de dois nós.

Por motivos análogos, cada nó também se encontra bem no meio de dois ventres.

A distância entre um nó e um ventre adjacentes vai ser um quarto do comprimento de onda:

d = λ 4

= 30 4

= 7,5 c m

= 7,5 × 10 - 2 m

A distância de nós ou ventres consecutivos é de 15cm, logo a menor distância entre um nó e um ventre é de 7,5cm.

“Faça seus medos terem medo de você”

Resposta

a )   15 c m

b )   30 c m , 0,43 c m ,   4 m / s

c )   0,71 2   m / s

v y , m í n = 0

d ) 7,5 c m

Exercícios de Livros Relacionados

Duas ondas, y 1 = 2,50 m m s e n [ 25,1 r a d m x - ( 440 r a d / s ) t ] y 2 = 1 , 50 m m s e n [ 25,1 r a d m x + ( 440 r a d / s ) t ] Propagam-se em uma corda esticada. (a) Plote a onda resultante
Duas cordas muito longas, bem esticadas, de densidades lineares diferentes μ 1 e μ 2 , estão ligadas uma à outra. Toma-se a posição de equilíbrio como eixo dos x e a origem O no ponto de junção, sendo
Suponha que o pulso que se desloca para a esquerda no Exercício 15.32 esteja abaixo do nível da corda não esticada, em vez de acima. Desenhe os mesmos diagramas que você desenhou naquele exercício.
As ondas estacionárias em um fio são descritas pela Equação 15.28, com A E S = 2,50 m m ,ω942 r a d / sek = 0,750 πr a d / m . A extremidade esquerda do fio está no ponto x=0 . Calcule as distâncias e