Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 14
Duas lâminas carregadas, infinitas e não condutora, são paralelas entre si, estando a lâmina no plano e lâmina no plano . Determine o campo elétrico na região , na região e entre as lâminas para as seguintes situações. (a) Quando cada lâmina tem uma densidade superficial uniforme de carga igual à e (b) quando a lâmina tem uma densidade superficial uniforme de carga igual à e lâmina uma densidade uniforme e igual à . (c) Esboce o padrão de linhas de campo elétrico para cada caso.
Passo 1
Inicialmente, lembre-se que o campo elétrico gerado por um plano infinito é sempre perpendicular ao plano e possui módulo dado por:
observe que o campo não depende da distância, ou seja, é uniforme!!
Passo 2
- Veja o esquema a seguir:
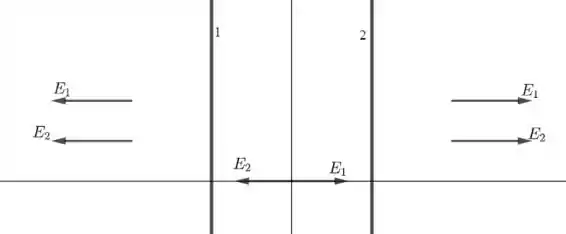
Notemos que
Assim,
- Para
- Para , temos
- Para , temos
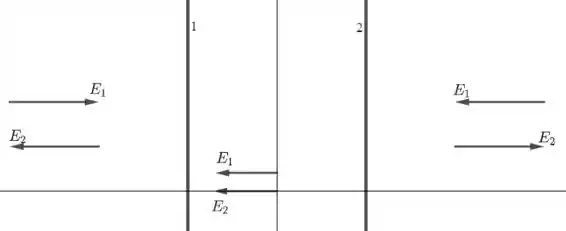
- Veja a figura a seguir:
- Para , temos
- Para , temos
- Para , temos
Passo 3
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Calcule o campo elétrico a uma distância z de um plano não condutor plano e infinito, uniformemente carregado, considerando o plano como um contínuo de infinitos anéis circulares de carga.
Uma linha de cargas com densidade linear uniforme λ está sobre o eixo x desde x = 0 até x = a . Mostre que a componente y do campo elétrico em um ponto do eixo y é dada por y = k λ y a y 2 + a 2 , y ≠
Calcule o campo elétrico a uma distância z de um plano não condutor plano e infinito, uniformemente carregado, considerando o plano como um contínuo de infinitas linhas retas de carga.
Uma linha de cargas com densidade linear uniforme λ está ao longo do eixo x desde x = x 1 até x = x 2 , onde x 1x 2 . Mostre que a componente x do campo elétrico em um ponto no eixo y é dado por E x =
Uma linha infinitamente longa de cargas tem densidade linear uniforme igual a - 1,50μ C / m e é paralelo ao eixo y em x = - 2,00m Uma crga puntiforme positiva igual a a 1,30μ C está localizada em x =