Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 23

Uma linha de cargas com densidade linear uniforme λ está sobre o eixo x desde x = 0 até x = a . Mostre que a componente y do campo elétrico em um ponto do eixo y é dada por y = k λ y a y 2 + a 2 , y ≠ 0 .

Passo 1

Veja a figura a seguir:

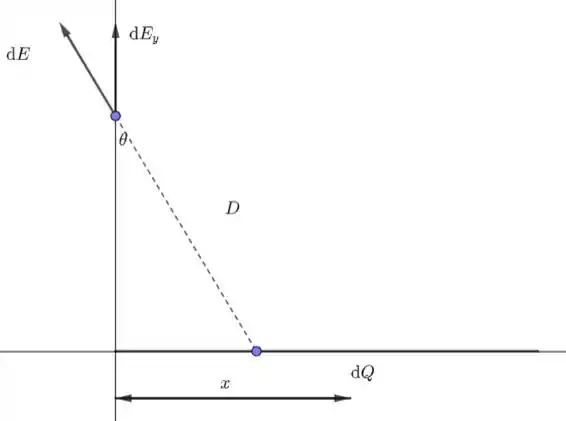
Temos que

d E = k   d Q D 2

onde

D = y sec ⁡ θ

e

x = y tg ⁡ θ ⟹ d x = y sec 2 ⁡ θ   d θ

Como

d Q = λ d x = λ y sec 2 ⁡ θ   d θ

Logo,

d E = k λ y sec 2 ⁡ θ   d θ   y 2 sec 2 ⁡ θ = k λ y d θ

Passo 2

Dessa forma, a componente y é:

d E y = d E cos ⁡ θ = k λ y cos ⁡ θ   d θ

Passo 3

Integrando, temos

E y = k λ y ∫ θ 1 θ 2 cos ⁡ θ   d θ = k λ y sen ⁡ θ 2 - sen ⁡ θ 1

onde

sen ⁡ θ 1 = 0

e

sen ⁡ θ 2 = a D = a a 2 + y 2

Segue então que:

E y = k λ y ⋅ a a 2 + y 2

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bastão de vidro com 10c m de comprimento está carregado uniformemente com+ 40n C . Uma pequena conta de vidro, carregada com + 6,0n C , encontra-se a 4,0c m do centro do bastão. Qual é a força (mód
Nos Problemas de 62 a 65, uma ou várias equações lhe são fornecidas para a resolução de um problema. Em cada uma das questões, Elabore um problema realista para o qual o conjunto de equações fornecido
Duas linhas de carga infinitas, cada qual com uma densidade linear de carga, estão posicionadas ao longo dos eixos x e y, passando ambas pela origem. Qual é a intensidade do campo elétrico na posição
A FIGURA P27.36 é uma secção transversal de duas linhas de carga infinitas que se estendem perpendicularmente para fora da página. Ambas possuem a mesma densidade linear de carga λ . Obtenha uma expre
Três bastões com 10 cm de comprimento cada formam um triângulo equilátero sobre um plano. Dois deles estão carregados com + 10n C , e o terceiro, com - 10n C . Qual é a intensidade do campo elétrico n