Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 24
Calcule o campo elétrico a uma distância de um plano não condutor plano e infinito, uniformemente carregado, considerando o plano como um contínuo de infinitas linhas retas de carga.
Passo 1
Veja a figura a seguir.
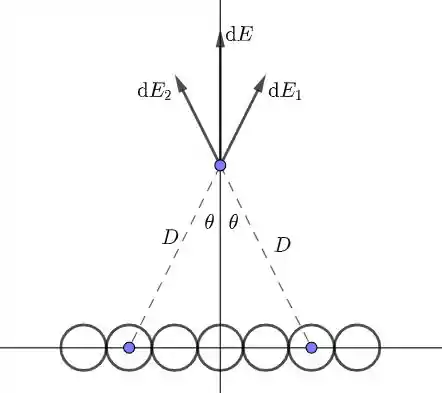
Aqui, os fios estão posicionados de maneira perpendicular à página (estamos vendo apenas uma seção do fio). Sabemos que cada fio produz um campo elétrico dado por:
Assim, vamos considerar o plano como sendo a função de infinitos fios. Suponha que cada fio tenha uma largura . Sendo o comprimento de cada fio, teremos:
Assim
Passo 2
Dessa forma, temos que
Da figura, temos que
e
Assim, segue que:
Analisando a figura, apenas a componente do campo elétrico não é cancelado. Assim,
Passo 3
Agora, bastará integrar de até (isso faz com que o número de fios aumente indefinidamente). Assim,
que é o valor que já conhecemos (veja como a lei de Gauss facilita muito a nossa vida nessa situação!!!).
Resposta
O campo elétrico vale